1. Definition:
Von einer algebraischen Funktion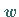 
einer komplexen Variablen 
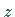spricht man, wenn
die Funktion das Ergebnis endlich vieler algebraischer Operationen mit dieser
Veränderlichen und eventuell noch mit endlich vielen Konstanten ist.
Ganz allgemein kann eine komplexe algebraische Funktion 
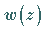wie ihr reelles Analogon
implizit als Polynom
 |
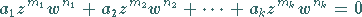(14.63) |
definiert werden.
Solche Funktionen müssen sich durchaus nicht immer nach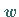
auflösen lassen.
2. Beispiele algebraischer Funktionen:
a) Lineare Funktion
 |
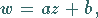(14.64) |
b) inverse Funktion
 |
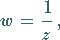(14.65) |
c) quadratische Funktion
 |
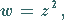(14.66) |
d) Quadratwurzelfunktion
 |
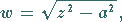(14.67) |
e) gebrochenlineare Funktion
 |
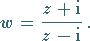(14.68) |
