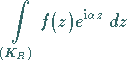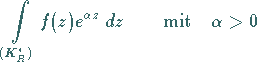In vielen Fällen lassen sich reelle uneigentliche Integrale mit unbeschränktem
Integrationsgebiet durch komplexe Integrale über geschlossene Wege berechnen.
Um dabei immer wiederkehrende Abschätzungen zu vermeiden, benutzt man das
Lemma von JORDAN , das sich auf Integrale der Form
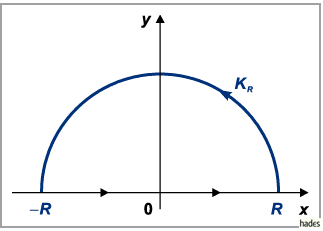
bezieht, wobei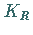 
der in der oberen Halbebene der 
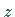-Ebene gelegene Halbkreisbogen
um den Nullpunkt mit dem Radius 
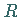ist (s. Abbildung).
Das Lemma von JORDAN unterscheidet folgende Fälle:
a)
:
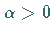Strebt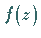 
in der oberen Halbebene und auf der reellen Achse für
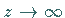gleichmäßig gegen Null und ist
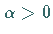eine positive Zahl, dann gilt für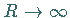 
 |
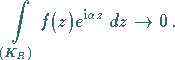(14.58a) |
b)
:
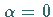Strebt der Ausdruck 
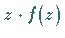für
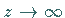gleichmäßig gegen
Null, dann gilt die Aussage (14.58a) auch im Falle 
.
c)
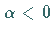: Liegt der Halbkreis unterhalb der
reellen Achse, dann gilt die entsprechende Aussage auch für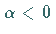 
.
d) Der Satz gilt auch, wenn es sich statt um einen vollen Halbkreis um
einen Teilbogen handelt.
e) Der entsprechende Sachverhalt liegt für Integrale der Form
 |
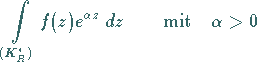(14.58b) |
vor, wenn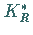 
einen Halbkreis bzw. Teilbogen in der linken Halbebene mit
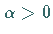darstellt, bzw in der rechten mit 
.
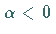