Integralsatz von Cauchy für einfach zusammenhängende Gebiete
Wenn eine Funktion 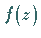 in einem einfach zusammenhängenden Gebiet analytisch ist,
dann gelten die folgenden zwei äquivalenten Aussagen:
in einem einfach zusammenhängenden Gebiet analytisch ist,
dann gelten die folgenden zwei äquivalenten Aussagen:
a) Das über eine geschlossene Kurve 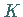 erstreckte Integral ist gleich Null:
erstreckte Integral ist gleich Null:
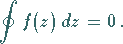 |
(14.40) |
b) Der Wert des Integrals 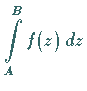 ist unabhängig von der
die Punkte
ist unabhängig von der
die Punkte 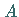 und
und 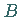 verbindenden Kurve.
verbindenden Kurve.
Dieser Sachverhalt wird Integralsatz von CAUCHY , auch
Hauptsatz der Funktionentheorie genannt.
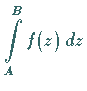 ist unabhängig von der
die Punkte
ist unabhängig von der
die Punkte ![]() und
und ![]() verbindenden Kurve.
verbindenden Kurve.