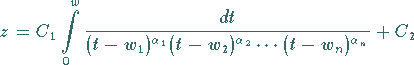|
|
|
|
 |
(14.19a) |
Außenwinkeln
der 
-Ebene auf die
obere 
-Halbebene abgebildet (s. Abbildung).
sind die den Ecken des Polygons zugeordneten Punkte der reellen Achse der
-Ebene bezeichnet, mit 
die Integrationsvariable.
Der orientierte, also durch eine Richtung ausgezeichnete Rand des Polygons geht bei der
Abbildung in die orientierte reelle Achse der -Ebene über.
Für große Werte von
verhält sich der Integrand wie 
und ist im
Unendlichen regulär.
Da die Summe aller Außenwinkel eines -Ecks gleich 
ist, gilt:
 |
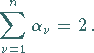(14.19b) |
und 
bewirken eine Drehstreckung und eine
Verschiebung, hängen aber nicht von der Form, sondern nur von Größe und Lage des
Polygons in der -Ebene ab.
-Ebene vorgegeben, dann können drei Punktpaare
willkürlich einander zugeordnet werden.
Ordnet man einem Eckpunkt des Polygons in der -Ebene, z.B. 
,
einen
unendlich fernen Punkt der -Ebene, also 
zu, dann ist der Faktor
wegzulassen.
Wenn das Polygon ausartet, z.B. dadurch, daß sich ein Eckpunkt im Unendlichen
befindet, dann ist der zugehörige Außenwinkel gleich 
,
also
,
d.h., das Polygon wird zum Halbstreifen.
| Beispiel A | |||||||||||||||||
|
Für das in der linken Abbildung skizzierte Gebiet der
Die Abbildungsformel lautet:  .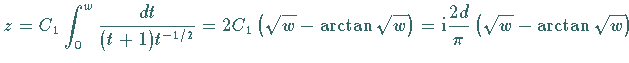
Bei der Bestimmung von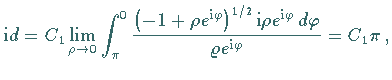
ist
zu setzen:
d.h.,  .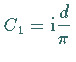
Daß die Konstante 
ist, geht aus der Zuordnung
,, `` hervor.
| |||||||||||||||||
| Beispiel B | |
|
Abbildung eines Rechtecks. Eckpunkte des abzubildenden Rechtecks seien
Damit lautet die Abbildungsformel für ein Rechteck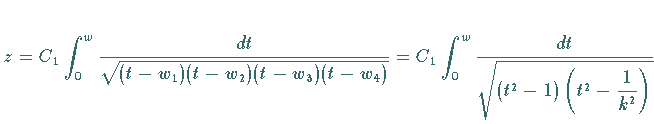 
der oben skizzierten Lage
 .
Punkt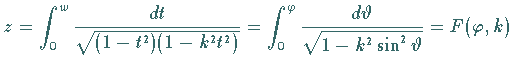 
entspricht Punkt 
und Punkt 
Punkt  .
Mit 
wird  ,
wobei die Substitution 
verwendet wurde.
Die Funktion 
ist ein elliptische Integral 1. Gattung.
Daß die Konstante
ist, geht aus der Zuordnung
,,`` hervor.
| |
|
|
angegebene Zuordnung dreier Punkte
gewählt.
.
Die Punkte 
und 
sollen in die Punkte 
und
der reellen Achse übergehen, 
und 
sind Spiegelpunkte zu 
und 
entsprechen (s. Abbildung).
