Beschreibung von Kurven in komplexer Form
Eine komplexe Funktion von einer reellen Veränderlichen 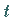 kann auch in
Parameterform dargestellt werden:
kann auch in
Parameterform dargestellt werden:
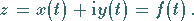 |
(14.91) |
Bei Änderungen von 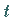 durchlaufen die Punkte
durchlaufen die Punkte 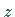 eine Kurve
eine Kurve 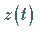 .
.
Die Gleichungen für Gerade, Kreis, Hyperbel, Ellipse und logarithmische Spirale lauten:
1. Gerade
a) Gerade durch einen Punkt
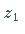 ,
Schnittwinkel
,
Schnittwinkel
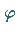 mit der
mit der
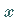 -Achse:
-Achse:
 |
(14.92a) |
b) Gerade durch zwei Punkte
 und
und
 :
:
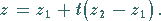 |
(14.92b) |
2. Kreis
a) Kreis, Radius 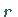 , Mittelpunkt im Koordinatenursprung:
, Mittelpunkt im Koordinatenursprung:
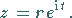 |
(14.93a) |
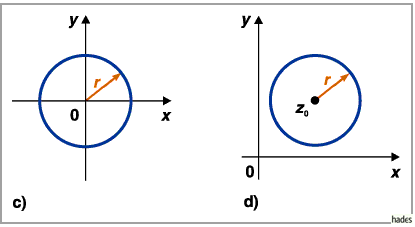
b) Kreis, Radius
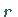 , Mittelpunkt im Punkt
, Mittelpunkt im Punkt
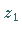 :
:
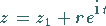 |
(14.93b) |
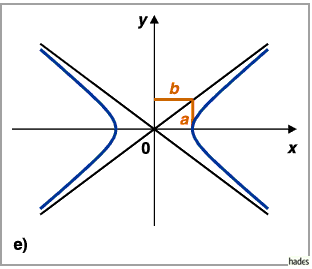
3. Hyperbel, Normalform
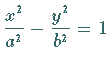
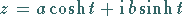 |
(14.94a) |
oder
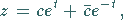 |
(14.94b) |
wobei 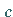 und
und 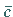 konjugiert komplexe Zahlen sind:
konjugiert komplexe Zahlen sind:
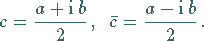 |
(14.94c) |
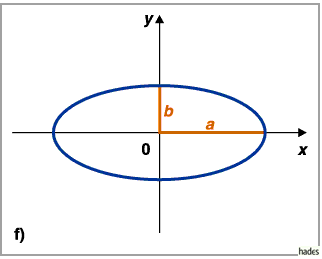
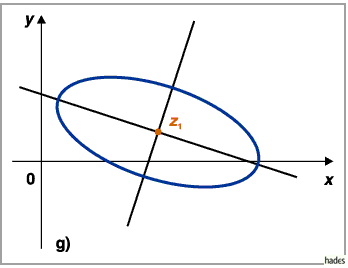
4. Ellipse
a) Ellipse, Normalform
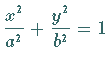 :
:
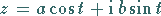 |
(14.95a) |
oder
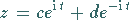 |
(14.95b) |
mit
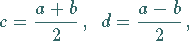 |
(14.95c) |
d.h., 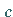 und
und 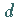 sind beliebige reelle Zahlen.
sind beliebige reelle Zahlen.
b) Ellipse, allgemeine Form: Der Mittelpunkt befindet sich im Punkt
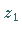 ,
die Achsen sind um einen Winkel gedreht.
,
die Achsen sind um einen Winkel gedreht.
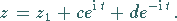 |
(14.96) |
Mit 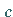 und
und 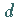 sind beliebige komplexe Zahlen bezeichnet, die die Länge der
Ellipsenachsen und ihre Drehung bestimmen.
sind beliebige komplexe Zahlen bezeichnet, die die Länge der
Ellipsenachsen und ihre Drehung bestimmen.
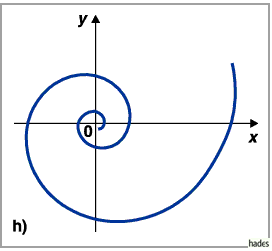
5. Logarithmische Spirale
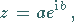 |
(14.97) |
wobei 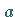 und
und 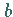 beliebige komplexe Zahlen sind.
beliebige komplexe Zahlen sind.
![]() ,
Schnittwinkel
,
Schnittwinkel
![]() mit der
mit der
![]() -Achse:
-Achse:
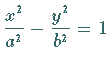
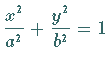 :
: