|
|
|
|
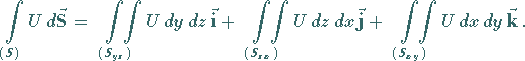 |
(13.113) |
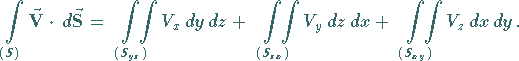 |
(13.114) |
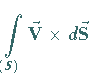 |
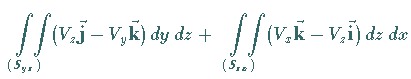 |
||
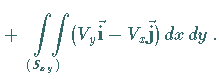 |
(13.115) |
Die Existenzsätze für diese Integrale können in Analogie zu den für
Oberflächenintegrale 2. Art angegebenen formuliert werden.
Bei der Berechnung der Zweifachintegrale werden zunächst die Projektionen von ![]() auf
die Koordinatenebenen gebildet (s. Abbildung), wobei eine der Variablen
auf
die Koordinatenebenen gebildet (s. Abbildung), wobei eine der Variablen
![]() oder
oder ![]() durch die beiden anderen mit Hilfe der Flächengleichung für
durch die beiden anderen mit Hilfe der Flächengleichung für ![]() ausgedrückt werden muß.
ausgedrückt werden muß.
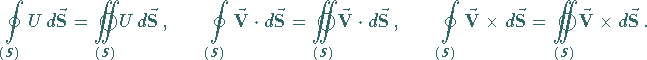 |
(13.116) |
| Beispiel A | |
|
Es ist | |
| Beispiel B | |
|
Es ist
| |
| Beispiel C | |
|
Es ist
| |
|
|
|