1. Einteilung des Weges 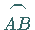 (s. Abbildung) durch Zwischenpunkte
(s. Abbildung) durch Zwischenpunkte
 in
in 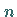 kleinere Teilbogenstücke, die
durch die Vektoren
kleinere Teilbogenstücke, die
durch die Vektoren 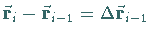 angenähert werden.
angenähert werden.
2. Wahl von Punkten 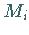 mit den Radiusvektoren
mit den Radiusvektoren 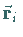 ,
die im Innern
oder auf dem Rande eines jeden Teilbogenstückes liegen können.
,
die im Innern
oder auf dem Rande eines jeden Teilbogenstückes liegen können.
3. Skalare Multiplikation der Funktionswerte 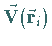 in den
so ausgewählten Punkten mit
in den
so ausgewählten Punkten mit  .
.
4. Addition aller auf diese Weise erhaltenen 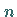 Produkte.
Produkte.
5. Berechnung des Grenzwertes der erhaltenen Summe
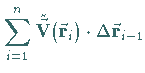 für
für
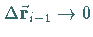 ,
also für
,
also für
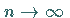 .
.
Wenn der Grenzwert existiert und von der Wahl der Punkte 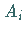 und
und 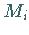 unabhängig ist,
dann wird er als Kurvenintegral
unabhängig ist,
dann wird er als Kurvenintegral
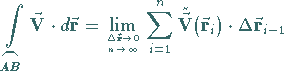 |
(13.96b) |
bezeichnet.
Die Existenz des Kurvenintegrals (13.96a,b) ist gesichert, wenn die
Vektorfunktion 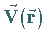 und das Bogenstück
und das Bogenstück 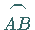 stetig sind
und wenn letzteres stetige Tangenten besitzt.
Eine Vektorfunktion
stetig sind
und wenn letzteres stetige Tangenten besitzt.
Eine Vektorfunktion 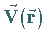 ist stetig, wenn die zu ihrer Beschreibung
notwendigen drei skalaren Funktionen, ihre Komponenten, stetig sind.
ist stetig, wenn die zu ihrer Beschreibung
notwendigen drei skalaren Funktionen, ihre Komponenten, stetig sind.
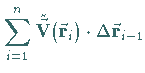 für
für
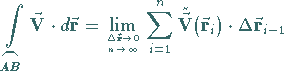
![]() und das Bogenstück
und das Bogenstück ![]() stetig sind
und wenn letzteres stetige Tangenten besitzt.
Eine Vektorfunktion
stetig sind
und wenn letzteres stetige Tangenten besitzt.
Eine Vektorfunktion ![]() ist stetig, wenn die zu ihrer Beschreibung
notwendigen drei skalaren Funktionen, ihre Komponenten, stetig sind.
ist stetig, wenn die zu ihrer Beschreibung
notwendigen drei skalaren Funktionen, ihre Komponenten, stetig sind.