Zu einem Vektorfeld 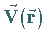 läßt sich ein zweites Vektorfeld,
seine Rotation bilden, indem die folgenden Schritte durchgeführt werden:
läßt sich ein zweites Vektorfeld,
seine Rotation bilden, indem die folgenden Schritte durchgeführt werden:
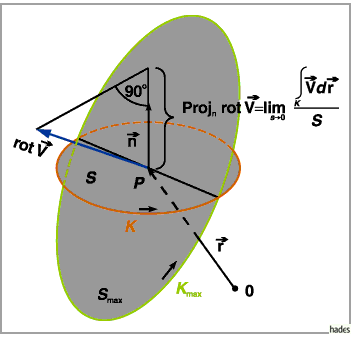
a) Aufspannen eines kleinen Flächenstückes 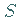 um den Punkt
um den Punkt 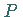 .
Dieses Flächenstück soll durch den Vektor
.
Dieses Flächenstück soll durch den Vektor 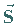 beschrieben werden, der in
die Richtung der Normalen
beschrieben werden, der in
die Richtung der Normalen  zeigt und dessen Betrag gleich dem Inhalt des
Fächenstückes ist. Der Rand des Flächenstückes sei mit
zeigt und dessen Betrag gleich dem Inhalt des
Fächenstückes ist. Der Rand des Flächenstückes sei mit 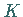 bezeichnet
(s. Abbildung).
bezeichnet
(s. Abbildung).
b) Berechnung des Umlaufintegrals
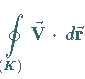 längs der Randkurve
längs der Randkurve 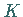 des
Flächenstücks.
des
Flächenstücks.
c) Untersuchung des Grenzwertes
wobei die Lage des Flächenstückes ungeändert bleibt.
d) Änderung der Lage des Flächenstückes mit dem Ziel, einen Maximalwert
des gewonnenen Grenzwertes zu ermitteln.
Das zugehörige Flächenstück habe den Flächeninhalt 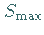 und die Randkurve
und die Randkurve
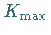 .
.
e) Bestimmung des Vektors 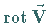 im Punkt
im Punkt  ,
dessen
Betrag gleich dem gefundenen Maximalwert des Grenzwertes ist und dessen Richtung mit der
Normalen des Flächenstückes zusammenfällt. Es gilt dann:
,
dessen
Betrag gleich dem gefundenen Maximalwert des Grenzwertes ist und dessen Richtung mit der
Normalen des Flächenstückes zusammenfällt. Es gilt dann:
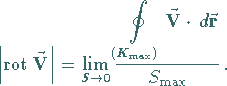 |
(13.56a) |
Die Projektion von 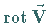 auf die Flächennormale
auf die Flächennormale  des
ursprünglichen Flächenstücks mit dem Inhalt
des
ursprünglichen Flächenstücks mit dem Inhalt 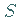 ,
d.h. die Komponente des
Vektors
,
d.h. die Komponente des
Vektors 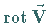 in beliebig vorgegebener Richtung
in beliebig vorgegebener Richtung 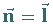 ,
ergibt sich zu
,
ergibt sich zu
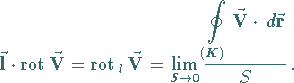 |
(13.56b) |
Die Feldlinien des Feldes 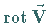 werden Wirbellinien des Vektorfeldes
werden Wirbellinien des Vektorfeldes
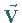 genannt.
genannt.
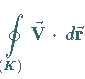 längs der Randkurve
längs der Randkurve 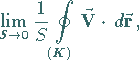
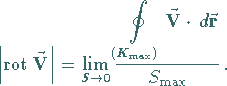
![]() auf die Flächennormale
auf die Flächennormale ![]() des
ursprünglichen Flächenstücks mit dem Inhalt
des
ursprünglichen Flächenstücks mit dem Inhalt ![]() ,
d.h. die Komponente des
Vektors
,
d.h. die Komponente des
Vektors ![]() in beliebig vorgegebener Richtung
in beliebig vorgegebener Richtung ![]() ,
ergibt sich zu
,
ergibt sich zu
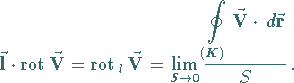
![]() werden Wirbellinien des Vektorfeldes
werden Wirbellinien des Vektorfeldes
![]() genannt.
genannt.