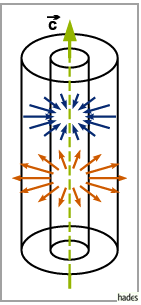
Zylindrisches Vektorfeld
a) Alle Vektoren 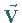 liegen auf Geraden, die auf einer bestimmten
Geraden, der Achse, senkrecht stehen und durch diese hindurchgehen, und
liegen auf Geraden, die auf einer bestimmten
Geraden, der Achse, senkrecht stehen und durch diese hindurchgehen, und
b) alle Vektoren 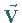 für Punkte, die gleichen Abstand von der Achse
haben, besitzen gleiche Beträge und sind entweder auf die Achse hin- oder von ihr
weggerichtet (s. Abbildung).
für Punkte, die gleichen Abstand von der Achse
haben, besitzen gleiche Beträge und sind entweder auf die Achse hin- oder von ihr
weggerichtet (s. Abbildung).
Wird der Koordinatenursprung auf die Achse gelegt, die durch den Vektor 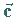 vorgegeben ist, dann kann dieses Feld durch die Formel
vorgegeben ist, dann kann dieses Feld durch die Formel
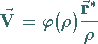 |
(13.15a) |
beschrieben werden.
Dabei ist 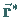 die Projektion von
die Projektion von  auf die Ebene, die auf der
Achse senkrecht steht:
auf die Ebene, die auf der
Achse senkrecht steht:
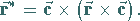 |
(13.15b) |
Jeder Schnitt dieses Feldes mit Ebenen, die senkrecht auf der Achse stehen, ergibt
gleichartige Kreisfelder.
![]() die Projektion von
die Projektion von ![]() auf die Ebene, die auf der
Achse senkrecht steht:
auf die Ebene, die auf der
Achse senkrecht steht: