Diskrete Quellenverteilung
In Analogie zur Überlagerung physikalischer Felder überlagern sich auch die
Vektorfelder der Mathematik.
Der Superpositionssatz lautet: Haben die Vektorfelder 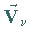 die
Potentiale
die
Potentiale 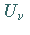 ,
so hat das Vektorfeld
,
so hat das Vektorfeld 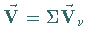 das Potential
das Potential 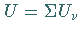 .
.
Für 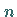 diskrete Quellpunkte mit den Ergiebigkeiten
diskrete Quellpunkte mit den Ergiebigkeiten
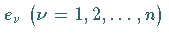 ,
deren Felder sich überlagern, kann man
daher das resultierende Feld durch algebraische Addition der Potentiale
,
deren Felder sich überlagern, kann man
daher das resultierende Feld durch algebraische Addition der Potentiale 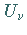 bestimmen:
bestimmen:
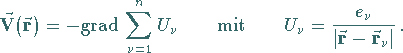 |
(13.129a) |
Dabei ist  wieder der Ortsvektor des Aufpunktes, während
wieder der Ortsvektor des Aufpunktes, während
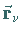 die Ortsvektoren der Quellpunkte sind.
die Ortsvektoren der Quellpunkte sind.
Treten wirbelfreie Felder 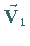 und quellenfreie Felder
und quellenfreie Felder 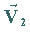 gemeinsam auf und handelt es sich dabei um überall stetige Felder, dann gilt:
gemeinsam auf und handelt es sich dabei um überall stetige Felder, dann gilt:
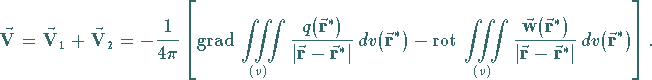 |
(13.129b) |
Erstreckt sich das Vektorfeld ins Unendliche, dann ist die Bestimmung von
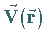 eindeutig, wenn
eindeutig, wenn 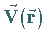 für
für
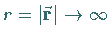 genügend stark verschwindet.
genügend stark verschwindet.
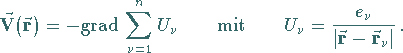
![]() wieder der Ortsvektor des Aufpunktes, während
wieder der Ortsvektor des Aufpunktes, während
![]() die Ortsvektoren der Quellpunkte sind.
die Ortsvektoren der Quellpunkte sind.
![]() und quellenfreie Felder
und quellenfreie Felder ![]() gemeinsam auf und handelt es sich dabei um überall stetige Felder, dann gilt:
gemeinsam auf und handelt es sich dabei um überall stetige Felder, dann gilt:
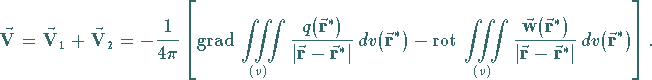
![]() eindeutig, wenn
eindeutig, wenn ![]() für
für
![]() genügend stark verschwindet.
genügend stark verschwindet.