Satz vom abgeschlossenen Graphen
Ein Operator 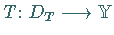 mit
mit 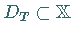 heißt
abgeschlossen , wenn aus
heißt
abgeschlossen , wenn aus 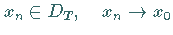 in
in  und
und
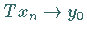 in
in 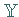 stets
stets 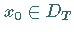 und
und 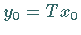 folgen.
Notwendig und hinreichend dafür ist die Abgeschlossenheit des Graphen des Operators
folgen.
Notwendig und hinreichend dafür ist die Abgeschlossenheit des Graphen des Operators  im Raum
im Raum 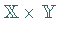 ,
d.h. der Menge
,
d.h. der Menge
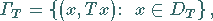 |
(12.143) |
wobei 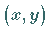 hier die Bezeichnung für ein Element der Menge
hier die Bezeichnung für ein Element der Menge 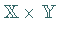 ist.
Es gilt: Ist
ist.
Es gilt: Ist  ein abgeschlossener Operator mit abgeschlossenem Definitionsbereich
ein abgeschlossener Operator mit abgeschlossenem Definitionsbereich
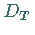 ,
dann ist
,
dann ist  stetig.
stetig.