Sei 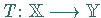 eine Abbildung des metrischen Raumes
eine Abbildung des metrischen Raumes
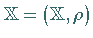 in den metrischen Raum
in den metrischen Raum 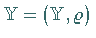 .
.
 heißt stetig im Punkt
heißt stetig im Punkt 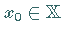 ,
wenn für jede Umgebung
,
wenn für jede Umgebung 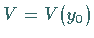 des Punktes
des Punktes 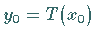 eine Umgebung
eine Umgebung 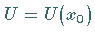 existiert, so daß gilt:
existiert, so daß gilt:
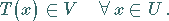 |
(12.74) |
 heißt stetig auf der Menge
heißt stetig auf der Menge 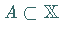 ,
wenn
,
wenn  in jedem Punkt der
Menge A stetig ist.
Äquivalente Eigenschaften zur Stetigkeit auf
in jedem Punkt der
Menge A stetig ist.
Äquivalente Eigenschaften zur Stetigkeit auf  sind:
sind:
a) Für einen beliebigen Punkt 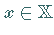 und eine beliebige Folge
und eine beliebige Folge
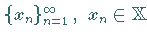 mit
mit 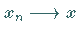 gilt stets
gilt stets
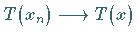 ,
also
,
also 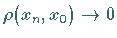 impliziert
impliziert
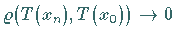 .
.
b) Für eine beliebige offene Teilmenge 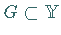 ist das Urbild
ist das Urbild 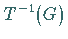 eine offene Teilmenge in
eine offene Teilmenge in 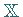 .
.
c) Für eine beliebige abgeschlossene Teilmenge 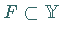 ist das Urbild
ist das Urbild
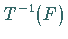 eine abgeschlossene Teilmenge in
eine abgeschlossene Teilmenge in 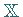 .
.
d) Für eine beliebige Teilmenge 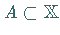 gilt
gilt
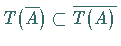 .
.
![]() heißt stetig auf der Menge
heißt stetig auf der Menge ![]() ,
wenn
,
wenn ![]() in jedem Punkt der
Menge A stetig ist.
Äquivalente Eigenschaften zur Stetigkeit auf
in jedem Punkt der
Menge A stetig ist.
Äquivalente Eigenschaften zur Stetigkeit auf ![]() sind:
sind:
![]() und eine beliebige Folge
und eine beliebige Folge
![]() mit
mit ![]() gilt stets
gilt stets
![]() ,
also
,
also ![]() impliziert
impliziert
![]() .
.
![]() ist das Urbild
ist das Urbild ![]() eine offene Teilmenge in
eine offene Teilmenge in ![]() .
.
![]() ist das Urbild
ist das Urbild
![]() eine abgeschlossene Teilmenge in
eine abgeschlossene Teilmenge in ![]() .
.
![]() gilt
gilt
![]() .
.