Begriff des Vektorraumes
Eine nichtleere Menge 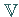 heißt Vektorraum oder linearer Raum über dem
Körper
heißt Vektorraum oder linearer Raum über dem
Körper 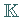 der Skalaren, wenn auf
der Skalaren, wenn auf 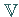 die beiden Operationen - Addition der Elemente
und Vielfachenbildung mit Koeffizienten aus
die beiden Operationen - Addition der Elemente
und Vielfachenbildung mit Koeffizienten aus 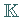 - wie folgt erklärt sind:
- wie folgt erklärt sind:
1. Für je zwei Elemente 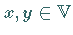 gibt es ein Element
gibt es ein Element 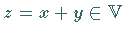 ,
ihre Summe ,
,
ihre Summe ,
2. für jedes 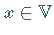 und jeden Skalar (Zahl)
und jeden Skalar (Zahl) 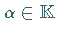 gibt es ein
Element
gibt es ein
Element 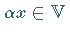 ,
das Produkt aus
,
das Produkt aus 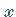 und dem Skalar
und dem Skalar 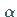 (oder besser, das
(oder besser, das 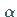 -Vielfache des Elements
-Vielfache des Elements 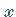 ),
),
so daß die folgenden Eigenschaften, die Vektorraumaxiome , für beliebige
Elemente 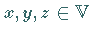 und Skalare
und Skalare 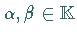 erfüllt sind:
erfüllt sind:
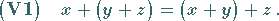 |
(12.1) |
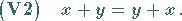 |
(12.2) |
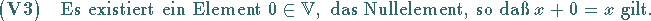 |
(12.3) |
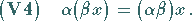 |
(12.4) |
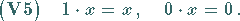 |
(12.5) |
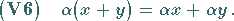 |
(12.6) |
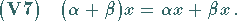 |
(12.7) |
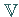 heißt reeller bzw. komplexer Vektorraum, je nachdem, ob
heißt reeller bzw. komplexer Vektorraum, je nachdem, ob 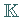 der Körper
der Körper 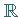 der reellen bzw.
der reellen bzw. 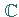 der komplexen Zahlen ist.
Die Elemente von
der komplexen Zahlen ist.
Die Elemente von 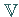 nennt man Punkte oder, in Anlehnung an die Lineare Algebra, auch
Vektoren , wobei in der Funktionalanalysis, ohne die Verständlichkeit oder die
Übersichtlichkeit zu beeinträchtigen, auf die Kennzeichnung
nennt man Punkte oder, in Anlehnung an die Lineare Algebra, auch
Vektoren , wobei in der Funktionalanalysis, ohne die Verständlichkeit oder die
Übersichtlichkeit zu beeinträchtigen, auf die Kennzeichnung 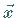 oder
oder
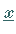 verzichtet wird.
verzichtet wird.
In einem Vektorraum 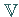 gibt es zu jedem
gibt es zu jedem 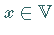 ein eindeutig bestimmtes
,,gegenüberliegendes`` Element
ein eindeutig bestimmtes
,,gegenüberliegendes`` Element 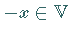 ,
so daß
,
so daß 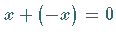 gilt, indem man
gilt, indem man 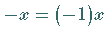 setzt.
Somit ist auf
setzt.
Somit ist auf 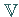 auch die Differenz
auch die Differenz 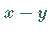 zweier beliebiger Vektoren
zweier beliebiger Vektoren 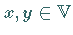 als
als 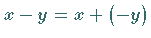 erklärt.
Daraus ergibt sich die eindeutige Lösbarkeit der Gleichung
erklärt.
Daraus ergibt sich die eindeutige Lösbarkeit der Gleichung 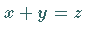 für vorgegebene
Elemente
für vorgegebene
Elemente 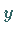 und
und 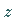 .
Die Lösung ist dann gleich
.
Die Lösung ist dann gleich 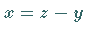 .
Aus den Axiomen (V1) bis (V7) ergeben sich die folgenden Eigenschaften:
.
Aus den Axiomen (V1) bis (V7) ergeben sich die folgenden Eigenschaften:
- Das Nullelement ist eindeutig definiert,
- falls
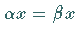 und
und 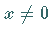 ,
dann
,
dann 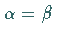 ,
,
- falls
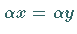 und
und 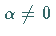 ,
dann
,
dann 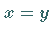 ,
,
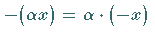 .
.
![]() gibt es zu jedem
gibt es zu jedem ![]() ein eindeutig bestimmtes
,,gegenüberliegendes`` Element
ein eindeutig bestimmtes
,,gegenüberliegendes`` Element ![]() ,
so daß
,
so daß ![]() gilt, indem man
gilt, indem man ![]() setzt.
Somit ist auf
setzt.
Somit ist auf ![]() auch die Differenz
auch die Differenz ![]() zweier beliebiger Vektoren
zweier beliebiger Vektoren ![]() als
als ![]() erklärt.
Daraus ergibt sich die eindeutige Lösbarkeit der Gleichung
erklärt.
Daraus ergibt sich die eindeutige Lösbarkeit der Gleichung ![]() für vorgegebene
Elemente
für vorgegebene
Elemente ![]() und
und ![]() .
Die Lösung ist dann gleich
.
Die Lösung ist dann gleich ![]() .
Aus den Axiomen (V1) bis (V7) ergeben sich die folgenden Eigenschaften:
.
Aus den Axiomen (V1) bis (V7) ergeben sich die folgenden Eigenschaften: