Komplexifikation reeller Vektorräume
Jeden reellen Vektorraum 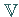 kann man zu einem komplexen Vektorraum
kann man zu einem komplexen Vektorraum 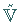 erweitern.
Die Menge
erweitern.
Die Menge 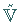 besteht aus allen Paaren
besteht aus allen Paaren 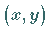 mit
mit 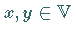 .
Die Operationen (Addition und Vielfaches mit einer komplexen Zahl
.
Die Operationen (Addition und Vielfaches mit einer komplexen Zahl 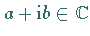 )
werden für diese Paare wie folgt festgelegt:
)
werden für diese Paare wie folgt festgelegt:
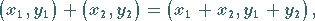 |
(12.22a) |
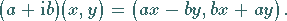 |
(12.22b) |
Da insbesondere
gilt, kann für das Paar 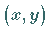 nun auch
nun auch 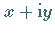 geschrieben werden.
Die Menge
geschrieben werden.
Die Menge 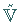 ist damit ein komplexer Vektorraum, in dem die Menge
ist damit ein komplexer Vektorraum, in dem die Menge 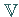 mit dem
linearen Teilraum
mit dem
linearen Teilraum 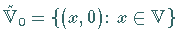 identifiziert
wird, also
identifiziert
wird, also 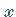 als
als 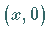 oder als
oder als 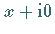 aufgefaßt wird.
aufgefaßt wird.
Die beschriebene Prozedur nennt man Komplexifikation
des Vektorraums 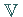 .
Eine linear unabhängige Teilmenge in
.
Eine linear unabhängige Teilmenge in 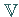 ist auch in
ist auch in 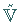 linear unabhängig.
Gleiches gilt für eine Basis in
linear unabhängig.
Gleiches gilt für eine Basis in 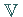 ,
woraus sich
,
woraus sich 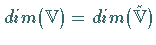 ergibt.
ergibt.
![]() nun auch
nun auch ![]() geschrieben werden.
Die Menge
geschrieben werden.
Die Menge ![]() ist damit ein komplexer Vektorraum, in dem die Menge
ist damit ein komplexer Vektorraum, in dem die Menge ![]() mit dem
linearen Teilraum
mit dem
linearen Teilraum ![]() identifiziert
wird, also
identifiziert
wird, also ![]() als
als ![]() oder als
oder als ![]() aufgefaßt wird.
aufgefaßt wird. ![]() .
Eine linear unabhängige Teilmenge in
.
Eine linear unabhängige Teilmenge in ![]() ist auch in
ist auch in ![]() linear unabhängig.
Gleiches gilt für eine Basis in
linear unabhängig.
Gleiches gilt für eine Basis in ![]() ,
woraus sich
,
woraus sich ![]() ergibt.
ergibt.