Der Begriff der meßbaren Funktion erfordert kein Maß, sondern eine
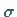-Algebra.
Seien 
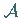eine 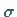-Algebra von Teilmengen der Menge 
und
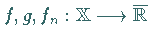meßbare Funktionen.
Dann sind auch die folgenden Funktionen (s. Vektorverbände) meßbar:
a)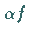 
für jedes 
.
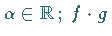b)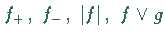 
und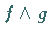 
;
c)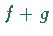 
,
falls in keinem Punkt von
ein Ausdruck der Form
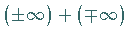vorkommt.
d)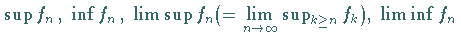 
.
e) der punktweise Grenzwert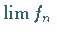 
,
im Falle seiner Existenz.
Eine Funktion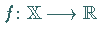 
heißt elementar oder
simpel, wenn es eine (endliche) Anzahl von paarweise disjunkten Mengen
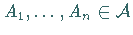und reelle Zahlen 
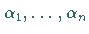gibt,
so daß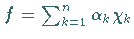 
gilt, wobei 
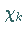die charakteristische
Funktion der Menge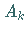 
bezeichnet.
Offenbar ist jede charakteristische Funktion einer meßbaren Menge und somit jede
elementare Funktion meßbar.
Interessant ist, daß jede meßbare Funktion beliebig genau durch
Elementarfunktionen approximiert werden kann:
Für jede meßbare Funktion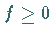 
existiert eine monoton wachsende Folge von
nichtnegativen Elementarfunktionen, die punktweise zu 
konvergiert.
