Lösungsansatz im Falle von Produktkernen
Die Auflösung FREDHOLMscher Integralgleichungen 2. Art mit ausgearteten Kernen
führt auf ein endlich dimensionales lineares Gleichungssystem.
Man betrachte die Integralgleichung
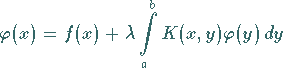 |
(11.4a) |
mit
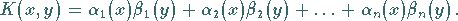 |
(11.4b) |
Die Funktionen 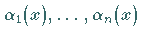 und
und 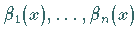 seien in dem Intervall
seien in dem Intervall 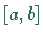 definiert und dort als stetig vorausgesetzt.
Weiterhin sollen die Funktionen
definiert und dort als stetig vorausgesetzt.
Weiterhin sollen die Funktionen 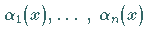 voneinander linear unabhängig sein, d.h., die Beziehung
voneinander linear unabhängig sein, d.h., die Beziehung
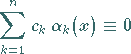 |
(11.5) |
mit konstanten Koeffizienten 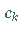 ist nur mit
ist nur mit 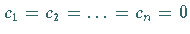 für alle
für alle 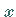 aus
aus
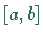 erfüllt.
erfüllt.
Aus (11.4a) und (11.4b) folgt:
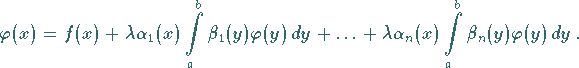 |
(11.6a) |
Die auftretenden Integrale hängen nicht mehr von der Variablen 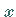 ab, sind also gewisse
konstante Werte, die mit
ab, sind also gewisse
konstante Werte, die mit 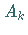 bezeichnet werden sollen:
bezeichnet werden sollen:
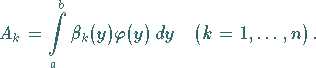 |
(11.6b) |
Die Lösungsfunktion 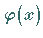 setzt sich, falls sie existiert, additiv aus der
Störfunktion
setzt sich, falls sie existiert, additiv aus der
Störfunktion 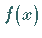 und einer Linearkombination der Funktionen
und einer Linearkombination der Funktionen
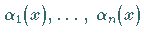 zusammen:
zusammen:
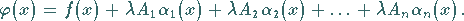 |
(11.6c) |
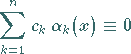
![]() ist nur mit
ist nur mit ![]() für alle
für alle ![]() aus
aus
![]() erfüllt.
erfüllt.