Eine der ersten Anwendungen von Integralgleichungen auf physikalische Probleme wurde von
ABEL untersucht.
In einer vertikalen Ebene bewege sich ein Massenpunkt entlang einer gewissen Kurve nur
unter dem Einfluß der Schwerkraft vom Punkt 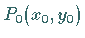 zum Punkt
zum Punkt 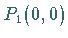 (s. Abbildung).
(s. Abbildung).
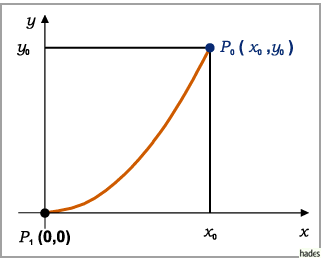
Die Geschwindigkeit des Teilchens in einem Punkt der Kurve beträgt
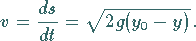 |
(11.74) |
Durch Integration ermittelt man die Fallzeit in Abhängigkeit von 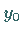 :
:
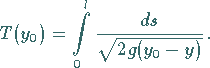 |
(11.75a) |
Stellt man 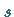 als Funktion von
als Funktion von 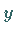 durch
durch 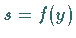 dar, so ist
dar, so ist
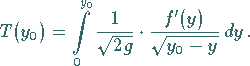 |
(11.75b) |
Es besteht nun die Aufgabe, zu gegebener Fallzeit die Gestalt der Kurve als Funktion von
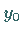 zu bestimmen.
Mit den Ersetzungen
zu bestimmen.
Mit den Ersetzungen
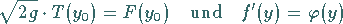 |
(11.75c) |
erhält man, indem noch die Variable 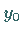 in
in 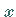 umbenannt wird, die
VOLTERRAsche Integralgleichung 1. Art
umbenannt wird, die
VOLTERRAsche Integralgleichung 1. Art
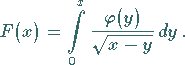 |
(11.75d) |
Es soll die etwas allgemeinere Gleichung
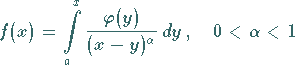 |
(11.76) |
behandelt werden.
Der Kern dieser Gleichung ist für 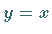 nicht beschränkt.
In (11.76) werden formal die Variable
nicht beschränkt.
In (11.76) werden formal die Variable 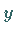 in
in 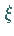 und die Variable
und die Variable
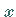 in
in 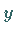 umbenannt.
Damit wird erreicht, daß sich die Lösung in der Form
umbenannt.
Damit wird erreicht, daß sich die Lösung in der Form 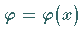 ergibt.
Die Multiplikation beider Seiten der Gleichung (11.76) mit dem Term
ergibt.
Die Multiplikation beider Seiten der Gleichung (11.76) mit dem Term
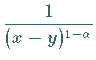 und die anschließende Integration nach
und die anschließende Integration nach 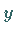 in den
Grenzen von
in den
Grenzen von 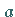 bis
bis 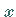 führt auf die Gleichung
führt auf die Gleichung
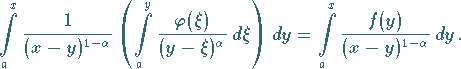 |
(11.77a) |
Die Vertauschung der Integrationsreihenfolge auf der linken Seite dieser Gleichung ergibt
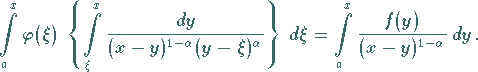 |
(11.77b) |
Das innere Integral ist mit der Substitution 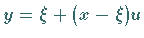 auswertbar:
auswertbar:
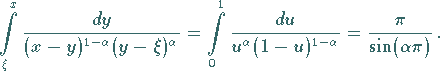 |
(11.77c) |
Der gewonnene Ausdruck wird in (11.77b) eingesetzt.
Die gesuchte Funktion 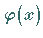 wird durch anschließende Differentiation nach
wird durch anschließende Differentiation nach 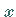 bestimmt:
bestimmt:
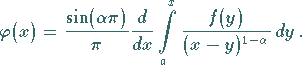 |
(11.77d) |
| Beispiel |
|
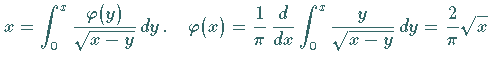 . .
|
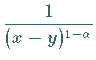 und die anschließende Integration nach
und die anschließende Integration nach ![]() wird durch anschließende Differentiation nach
wird durch anschließende Differentiation nach ![]() bestimmt:
bestimmt: