Ist die gesuchte Funktion in allen Termen nur linear enthalten, dann spricht man von einer
linearen Integralgleichung .
Die allgemeine Form einer linearen Integralgleichung lautet:
 |
(11.1) |
Die Funktion 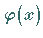 ist zu bestimmen, die Funktion
ist zu bestimmen, die Funktion 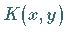 heißt
Kern der Integralgleichung und
heißt
Kern der Integralgleichung und 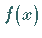 ihre Störfunktion .
Diese Funktionen können auch komplexe Werte annehmen.
Verschwindet die Funktion
ihre Störfunktion .
Diese Funktionen können auch komplexe Werte annehmen.
Verschwindet die Funktion 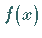 in dem betrachteten Bereich, d.h., ist
in dem betrachteten Bereich, d.h., ist 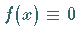 ,
dann ist es eine homogene Integralgleichung , andernfalls eine inhomogene .
Die Größe
,
dann ist es eine homogene Integralgleichung , andernfalls eine inhomogene .
Die Größe 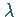 ist ein im allgemeinen komplexwertiger Parameter .
ist ein im allgemeinen komplexwertiger Parameter .
Zwei Spezialfälle von (11.1) haben besondere Bedeutung.
Sind die Integrationsgrenzen unabhängig von 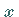 ,
also konstante Größen, d.h.
,
also konstante Größen, d.h.
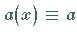 und
und 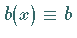 ,
dann handelt es sich um eine FREDHOLMsche
Integralgleichung:
,
dann handelt es sich um eine FREDHOLMsche
Integralgleichung:
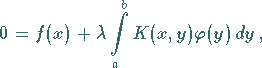 |
(11.2a) |
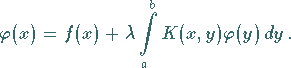 |
(11.2b) |
Ist 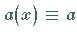 und
und 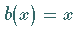 ,
so spricht man von einer VOLTERRAschen
Integralgleichung:
,
so spricht man von einer VOLTERRAschen
Integralgleichung:
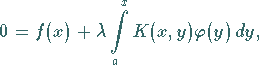 |
(11.2c) |
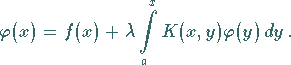 |
(11.2d) |
Kommt die zu ermittelnde Funktion 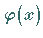 nur unter dem Integral vor, d.h. ist
nur unter dem Integral vor, d.h. ist
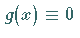 ,
dann liegt eine Integralgleichung 1. Art vor (11.2a,
11.2c).
Eine Integralgleichung 2. Art ist durch
,
dann liegt eine Integralgleichung 1. Art vor (11.2a,
11.2c).
Eine Integralgleichung 2. Art ist durch 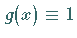 gekennzeichnet
(11.2b,11.2d).
gekennzeichnet
(11.2b,11.2d).
Hinweis: In diesem Kapitel werden nur Integralgleichungen 1. und 2. Art vom
FREDHOLMschen und VOLTERRAschen Typ betrachtet sowie einige singuläre
Intgralgleichungen.
![]() ,
also konstante Größen, d.h.
,
also konstante Größen, d.h.
![]() und
und ![]() ,
dann handelt es sich um eine FREDHOLMsche
Integralgleichung:
,
dann handelt es sich um eine FREDHOLMsche
Integralgleichung: