Zur FREDHOLMschen Integralgleichung 2. Art
 |
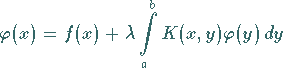(11.21a) |
ist durch
 |
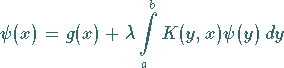(11.21b) |
eine zugehörige transponierte Integralgleichung gegeben.
Zu diesem Paar von Integralgleichungen lassen sich folgende Aussagen treffen
(s. auch Integralgleichungen mit ausgearteten Kernen).
1. Eine FREDHOLMsche Integralgleichung 2. Art besitzt nur abzählbar viele
Eigenwerte, welche sich nur im Unendlichen häufen können, d.h., es existieren für
jede reelle Zahl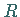 
nur endlich viele Eigenwerte 
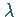mit 
.
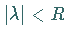2. Ist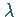
kein Eigenwert von (11.21a), dann sind beide inhomogene
Integralgleichungen für beliebige Störfunktionen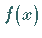 
bzw.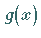 
eindeutig
lösbar, und die zugehörigen homogenen Integralgleichungen besitzen nur die triviale
Lösung.
3. Ist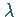
ein Eigenwert von (11.21a), dann ist
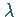auch
Eigenwert der transponierten Gleichung (11.21b).
Beide homogene Integralgleichungen haben dann nicht verschwindende Lösungen, und die
Anzahl linear unabhängiger Eigenfunktionen stimmt für beide Gleichungen überein.
4. Eine inhomogene Integralgleichung ist genau dann lösbar, wenn die
Störfunktion zu allen Lösungen der homogenen transponierten Integralgleichung
orthogonal ist, d.h. falls für alle Lösungen der Integralgleichung
 |
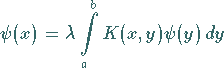(11.22a) |
gilt
 |
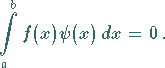(11.22b) |
Aus diesen Sätzen folgt der FREDHOLMsche Alternativsatz :
Entweder die inhomogene Integralgleichung ist für beliebige Störfunktion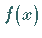
lösbar oder die zugehörige homogene Gleichung besitzt nichttriviale Lösungen.
