Eine FREDHOLMsche Integralgleichung 2. Art
 |
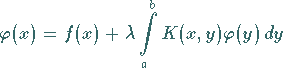(11.15) |
kann näherungsweise in Form eines linearen Gleichungssystems dargestellt werden.
Es sei vorausgesetzt, daß die Funktionen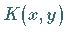 
und 
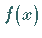für
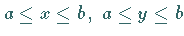stetig sind.
Das Integral in (11.15) soll durch die
linksseitige Rechteckformel angenähert werden.
Man könnte aber auch eine beliebige andere Quadraturformel anwenden.
Mit den äquidistanten Punkten
 |
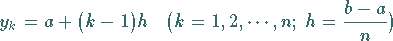(11.16a) |
erhält man die Näherung
 |
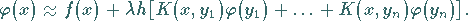(11.16b) |
Man ersetzt in dieser Beziehung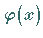 
durch eine Funktion
,
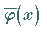die (11.16b) exakt erfüllt:
 |
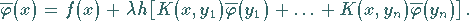(11.16c) |
Zur Auswertung dieser Näherungslösung benötigt man die Funktionswerte der Funktion
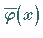in den Stützstellen 
.
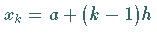Setzt man in (11.16c) nacheinander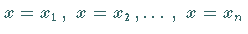 
,
so erhält man ein lineares Gleichungssystem für die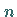 
gesuchten Funktionswerte
.
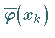Mit den Abkürzungen
 |
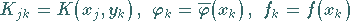(11.17a) |
lautet dieses Gleichungssystem
 |
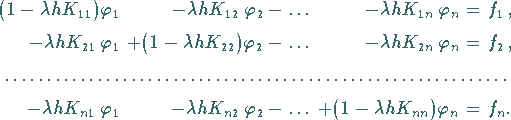(11.17b) |
Das System besitzt die Koeffizientendeterminante
 |
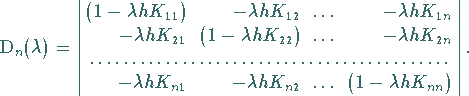(11.17c) |
Diese Determinante hat dieselbe Struktur wie die Koeffizientendeterminante, die bei der
Behandlung von Integralgleichungen mit ausgearteten Kernen auftritt.
Das Gleichungssystem (11.17b) besitzt eine eindeutige Lösung für alle
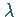mit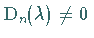 
.
Diese Lösung besteht aus Näherungen für die Funktionswerte der gesuchten Funktion
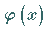in den Stützstellen.
Die Zahlen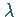
mit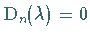 
sind Näherungen für die Eigenwerte
der Integralgleichung.
Die Lösung von (11.17b) läßt sich gemäß der
CRAMERschen Regel als Quotient darstellen:
 |
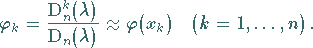(11.18) |
Dabei entsteht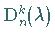 
aus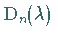 
,
indem die 
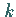-te
Spalte durch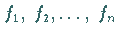 
ersetzt wird.
