1. Arithmetische Reihe 1. Ordnung
heißt die Reihe (1.54), wenn die
Differenz von je zwei aufeinanderfolgenden Summanden konstant ist, d.h. wenn gilt:
 |
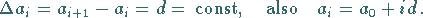(1.55a) |
Somit wird
 |
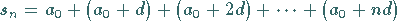(1.55b) |
mit dem Summenwert
 |
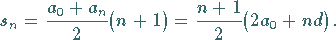(1.55c) |
2. Arithmetische Reihe k-ter Ordnung
heißt eine Reihe, wenn die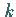 
-ten
Differenzen 
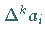der Folge 
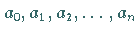konstant sind.
Die Differenzen höherer Ordnung werden rekursiv durch
 |
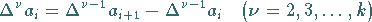(1.56a) |
gebildet.
Sie ergeben sich bequem aus dem folgenden Differenzenschema :
Es gilt dann für die Glieder und für die Summe
 |
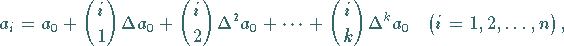(1.56c) |
 |
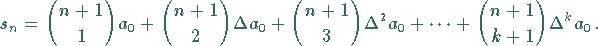(1.56d) |
