Graphische Differentiation
Wenn eine differenzierbare Funktion 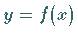 durch ihre Kurve
durch ihre Kurve 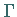 in kartesischen
Koordinaten in einem Intervall
in kartesischen
Koordinaten in einem Intervall 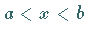 dargestellt ist, kann die Kurve
dargestellt ist, kann die Kurve 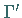 ihrer
Ableitung näherungsweise konstruiert werden.
Die Konstruktion einer Tangente in einem gegebenen Kurvenpunkt nach Augenmaß kann
recht ungenau ausfallen.
Wenn aber die Richtung der Tangente
ihrer
Ableitung näherungsweise konstruiert werden.
Die Konstruktion einer Tangente in einem gegebenen Kurvenpunkt nach Augenmaß kann
recht ungenau ausfallen.
Wenn aber die Richtung der Tangente 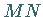 (s. Abbildung) bekannt ist, kann der
Berührungspunkt
(s. Abbildung) bekannt ist, kann der
Berührungspunkt 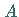 genauer ermittelt werden.
genauer ermittelt werden.
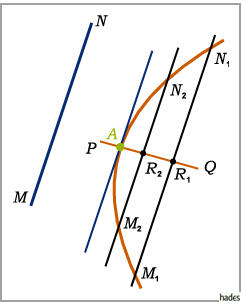
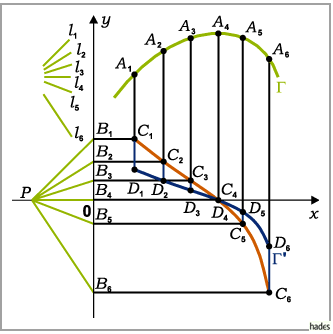
a) Konstruktion des Berührungspunktes einer Tangente:
Parallel zur gegebenen Tangentenrichtung 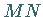 werden zwei Sehnen
werden zwei Sehnen 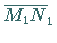 und
und
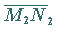 so eingezeichnet, daß die Kurve in nicht weit voneinander
liegenden Punkten geschnitten wird.
Danach werden die Mittelpunkte der Sehnen ermittelt und durch diese eine Gerade
so eingezeichnet, daß die Kurve in nicht weit voneinander
liegenden Punkten geschnitten wird.
Danach werden die Mittelpunkte der Sehnen ermittelt und durch diese eine Gerade 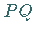 gezogen, die die Kurve im Punkt
gezogen, die die Kurve im Punkt 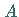 schneidet, in dem die Tangente näherungsweise die
vorgegebene Richtung
schneidet, in dem die Tangente näherungsweise die
vorgegebene Richtung 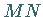 hat.
Um die Genauigkeit zu überprüfen, kann eine dritte Sehne in geringem Abstand von den
ersten beiden eingetragen werden, die von der Geraden
hat.
Um die Genauigkeit zu überprüfen, kann eine dritte Sehne in geringem Abstand von den
ersten beiden eingetragen werden, die von der Geraden 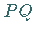 im Mittelpunkt geschnitten
werden muß.
im Mittelpunkt geschnitten
werden muß.
b) Konstruktion der Kurve einer abgeleiteten Funktion:
1. Vorgabe einiger Richtungen 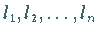 ,
die den Tangentenrichtungen
der Kurve
,
die den Tangentenrichtungen
der Kurve 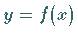 in dem betrachteten Intervall entsprechen sollen (s. Abbildung),
und Ermittlung der dazugehörigen Berührungspunkte
in dem betrachteten Intervall entsprechen sollen (s. Abbildung),
und Ermittlung der dazugehörigen Berührungspunkte 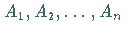 nach dem
unter a) beschriebenen Verfahren, wobei die Tangenten selbst nicht konstruiert werden
müssen.
nach dem
unter a) beschriebenen Verfahren, wobei die Tangenten selbst nicht konstruiert werden
müssen.
2. Wahl eines Punktes 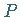 ,
eines ,,Pols``, auf der negativen
,
eines ,,Pols``, auf der negativen 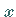 -Achse,
wobei die Strecke
-Achse,
wobei die Strecke 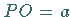 um so größer sein soll, je flacher die Kurve ist.
um so größer sein soll, je flacher die Kurve ist.
3. Einzeichnen von Geraden, die parallel zu den Richtungen 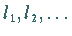 bzw.
bzw.
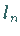 verlaufen, durch den Pol
verlaufen, durch den Pol 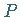 hindurchgehen und die
hindurchgehen und die 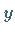 -Achse in den Punkten
-Achse in den Punkten
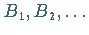 bzw.
bzw. 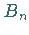 schneiden.
schneiden.
4. Konstruktion horizontaler Geraden 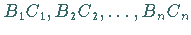 von den
Punkten
von den
Punkten 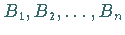 aus bis zu den Schnittpunkten
aus bis zu den Schnittpunkten 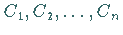 mit den aus den Punkten
mit den aus den Punkten 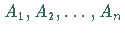 gefällten Loten.
gefällten Loten.
5. Verbinden der Punkte 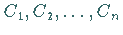 mit Hilfe eines Kurvenlineals
durch eine Kurve, die der Gleichung
mit Hilfe eines Kurvenlineals
durch eine Kurve, die der Gleichung 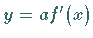 genügt.
Wenn die Strecke
genügt.
Wenn die Strecke 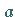 so gewählt wird, daß sie der Längeneinheit auf der
so gewählt wird, daß sie der Längeneinheit auf der 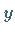 -Achse
entspricht, ist die gewonnene Kurve die der gesuchten Ableitung.
Ist das nicht der Fall, dann sind die gefundenen Ordinaten
-Achse
entspricht, ist die gewonnene Kurve die der gesuchten Ableitung.
Ist das nicht der Fall, dann sind die gefundenen Ordinaten 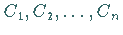 der
Ableitung mit dem Faktor
der
Ableitung mit dem Faktor 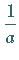 zu multiplizieren.
Die sich so ergebenden Punkte
zu multiplizieren.
Die sich so ergebenden Punkte 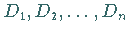 in der rechten Abbildung liegen
auf der maßstabsgerechten Ableitungskurve
in der rechten Abbildung liegen
auf der maßstabsgerechten Ableitungskurve  .
.