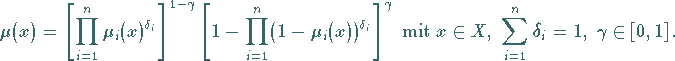Kompensatorische Operatoren
Gelegentlich benötigt man Operatoren, die zwischen den 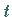 - und
- und 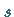 -Normen liegen;
sie werden kompensatorische Operatoren genannt.
Beispiele für kompensatorische Operatoren sind der Lambda- und der Gamma-Operator.
-Normen liegen;
sie werden kompensatorische Operatoren genannt.
Beispiele für kompensatorische Operatoren sind der Lambda- und der Gamma-Operator.
1. Lambda-Operator:
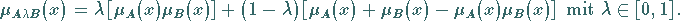 |
(5.369) |
Fall  Die Gleichung (5.369) liefert eine Form, die als algebraische Summe bekannt ist
(s. Tabelle der
Die Gleichung (5.369) liefert eine Form, die als algebraische Summe bekannt ist
(s. Tabelle der 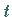 - und
- und 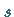 -Normen,
-Normen, 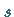 -Normen); ihr ist der
ODER-Operator zuzuordnen.
-Normen); ihr ist der
ODER-Operator zuzuordnen.
Fall  Die Gleichung (5.369) liefert eine Form, die als algebraisches Produkt bekannt
ist (s. Tabelle der
Die Gleichung (5.369) liefert eine Form, die als algebraisches Produkt bekannt
ist (s. Tabelle der 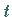 - und
- und 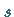 -Normen,
-Normen, 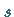 -Normen); ihr ist der
UND-Operator zuzuordnen.
-Normen); ihr ist der
UND-Operator zuzuordnen.
2. Gamma-Operator:
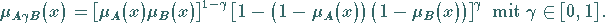 |
(5.370) |
Fall 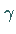 = 1: liefert die Darstellung für die algebraische Summe.
= 1: liefert die Darstellung für die algebraische Summe.
Fall 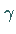 = 0: liefert die Darstellung für das algebraische Produkt.
= 0: liefert die Darstellung für das algebraische Produkt.
Die Anwendung des Gamma-Operators auf beliebig viele unscharfe Mengen ist gegeben durch
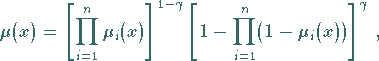 |
(5.371) |
und mit einer Wichtung 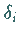 versehen ergibt sich:
versehen ergibt sich:
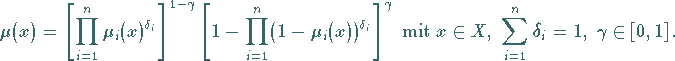 |
(5.372) |
![]() = 1: liefert die Darstellung für die algebraische Summe.
= 1: liefert die Darstellung für die algebraische Summe.
![]() = 0: liefert die Darstellung für das algebraische Produkt.
= 0: liefert die Darstellung für das algebraische Produkt.
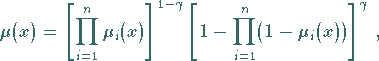
![]() versehen ergibt sich:
versehen ergibt sich: