RSA-Verfahren
Das im Kapitel Zahlentheorie beschriebene RSA-Verfahren ist das
populärste asymmetrische Verschlüsselungsverfahren.
1. Voraussetzungen: Man wählt zwei große Primzahlen 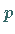 und
und 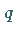 und
und
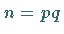 .
Dabei soll
.
Dabei soll 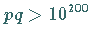 gelten;
gelten; 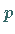 und
und 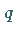 müssen sich als Dezimalzahlen in ihrer
Länge um einige Stellen unterscheiden; die Differenz zischen
müssen sich als Dezimalzahlen in ihrer
Länge um einige Stellen unterscheiden; die Differenz zischen 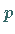 und
und 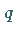 darf aber
auch nicht zu groß sein.
Weiterhin sollen
darf aber
auch nicht zu groß sein.
Weiterhin sollen 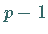 und
und 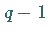 große Primfaktoren enthalten, und der größte
gemeinsame Teiler von
große Primfaktoren enthalten, und der größte
gemeinsame Teiler von 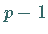 und
und 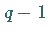 soll möglichst klein sein.
Man wähle ein
soll möglichst klein sein.
Man wähle ein 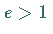 ,
das teilerfremd zu
,
das teilerfremd zu 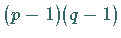 ist, und berechne ein
ist, und berechne ein 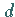 mit
mit
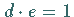 modulo
modulo 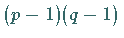 .
Dann bilden
.
Dann bilden  und
und 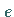 den öffentlichen Schlüssel und
den öffentlichen Schlüssel und 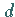 den privaten Schlüssel.
den privaten Schlüssel.
2. Verschlüsselungsoperation:
 |
(5.290a) |
3. Entschlüsselungsoperation:
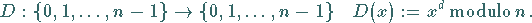 |
(5.290b) |
Damit gilt 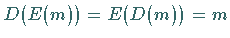 für jede Nachricht
für jede Nachricht 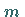 .
.
Die zur Verschlüsselung verwendete Funktion ist für 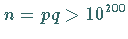 ein Kandidat für
eine
ein Kandidat für
eine
Einwegfunktion mit Falltür.
Die Zusatzinformation liegt hier in der Kenntnis der Primfaktorenzerlegung von 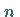 .
Ohne diese Information ist es praktisch unmöglich, die Kongruenz
.
Ohne diese Information ist es praktisch unmöglich, die Kongruenz
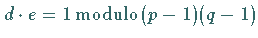 zu lösen.
zu lösen.
Das RSA-Verfahren gilt weithin als praktisch sicher, sofern die oben genannten
Bedingungen erfüllt sind.
Als Nachteil gegenüber anderen Verfahren sind die relativ große Schlüssellänge
und die Tatsache zu beachten, daß RSA gegenüber DES um etwa den Faktor 1000
langsamer ist.
![]() ein Kandidat für
eine
ein Kandidat für
eine ![]() .
Ohne diese Information ist es praktisch unmöglich, die Kongruenz
.
Ohne diese Information ist es praktisch unmöglich, die Kongruenz
![]() zu lösen.
zu lösen.