Krümmung von Kurven auf einer Fläche
Wenn durch einen Flächenpunkt  verschiedene Kurven
verschiedene Kurven  auf dieser Fläche
gezogen werden, dann stehen ihre Krümmungskreisradien
auf dieser Fläche
gezogen werden, dann stehen ihre Krümmungskreisradien  im Punkt
im Punkt  in den
folgenden drei Beziehungen zueinander (s. die folgenden Abbildungen):
in den
folgenden drei Beziehungen zueinander (s. die folgenden Abbildungen):
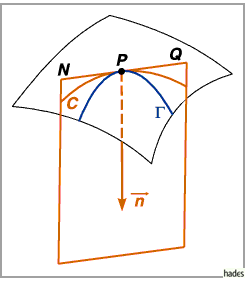
1. Krümmungskreisradius: Der Krümmungskreisradius 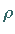 einer Kurve
einer Kurve
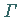 im Punkt
im Punkt  ist gleich dem Krümmungskreisradius einer Kurve
ist gleich dem Krümmungskreisradius einer Kurve
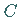 ,
die sich als Schnitt der Fläche mit der Schmiegungsebene der Kurve
,
die sich als Schnitt der Fläche mit der Schmiegungsebene der Kurve
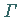 im Punkt
im Punkt 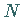 ergibt (linke Abbildung).
ergibt (linke Abbildung).
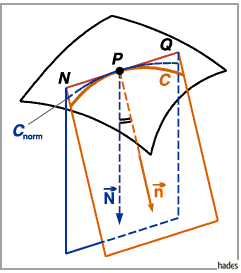
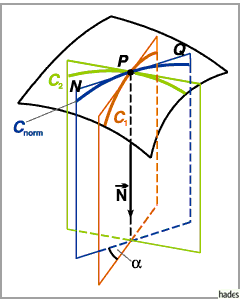
2. Satz von Meusnier: Für jeden ebenen Schnitt 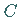 durch eine Fläche
(rechte Abbildung) berechnet man den Krümmungskreisradius
durch eine Fläche
(rechte Abbildung) berechnet man den Krümmungskreisradius 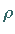 gemäß
gemäß
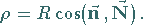 |
(3.527) |
Dabei ist 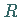 der Krümmungskreisradius des Normalschnittes
der Krümmungskreisradius des Normalschnittes  der
durch die gleiche Tangente
der
durch die gleiche Tangente 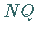 geht wie
geht wie 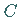 sowie durch den Einheitsvektor
sowie durch den Einheitsvektor 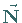 der Flächennormalen;
der Flächennormalen; 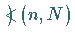 ist der Winkel zwischen dem Einheitsvektor
ist der Winkel zwischen dem Einheitsvektor
 der Hauptnormalen der Kurve
der Hauptnormalen der Kurve 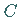 und dem Einheitsvektor
und dem Einheitsvektor 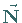 der
Flächennormalen.
Das Vorzeichen von
der
Flächennormalen.
Das Vorzeichen von 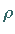 in (3.527) ist positiv, wenn
in (3.527) ist positiv, wenn 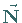 auf der konkaven Seite der Kurve
auf der konkaven Seite der Kurve  liegt und negativ im umgekehrten Falle.
liegt und negativ im umgekehrten Falle.
3. Eulersche Formel: Die Krümmung eines jeden Normalschnittes
 kann mit der Formel von EULER
kann mit der Formel von EULER
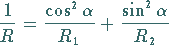 |
(3.528) |
berechnet werden, wobei 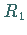 und
und 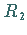 die Hauptkrümmungskreisradien
sind, und
die Hauptkrümmungskreisradien
sind, und 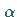 ist der Winkel zwischen den Ebenen der Schnitte
ist der Winkel zwischen den Ebenen der Schnitte 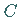 und
und 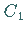 (untere Abbildung).
(untere Abbildung).