Schnittwinkel, Kurswinkel und Azimut
Schnittwinkel und Kurswinkel: Unter dem Schnittwinkel zweier sphärischer
Kurven versteht man den Winkel, den ihre Tangenten im Kurvenschnittpunkt 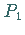 bilden.
Ist eine der beiden Kurven ein Meridian, dann wird der Schnittwinkel der nördlich von
bilden.
Ist eine der beiden Kurven ein Meridian, dann wird der Schnittwinkel der nördlich von
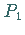 gelegenen Kurvenabschnitte in der Navigation Kurswinkel
gelegenen Kurvenabschnitte in der Navigation Kurswinkel 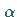 genannt.
Zur Beschreibung der östlichen und westlichen Neigung der Kurve ordnet man dem
Kurswinkel gemäß Teil a) und b) der Abbildung ein Vorzeichen zu und beschränkt
ihn auf das Intervall
genannt.
Zur Beschreibung der östlichen und westlichen Neigung der Kurve ordnet man dem
Kurswinkel gemäß Teil a) und b) der Abbildung ein Vorzeichen zu und beschränkt
ihn auf das Intervall 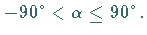
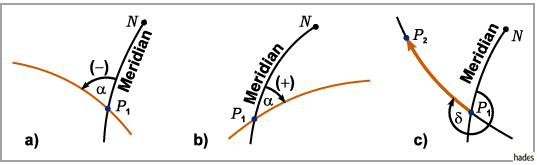
Kurswinkel und Azimut: Der Kurswinkel ist ein orientierter, d.h. mit einem
Vorzeichen versehener Winkel.
Er ist unabhängig von der Orientierung der Kurve - das ist ihr Durchlaufsinn.
Die Orientierung der Kurve von 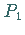 nach
nach 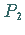 gemäß Teil c) der Abbildung wird
durch das Azimut
gemäß Teil c) der Abbildung wird
durch das Azimut 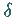 beschrieben:
Es ist der Schnittwinkel zwischen dem durch den Kurvenschnittpunkt
beschrieben:
Es ist der Schnittwinkel zwischen dem durch den Kurvenschnittpunkt 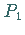 verlaufenden und
nach Norden weisenden Meridian und dem von
verlaufenden und
nach Norden weisenden Meridian und dem von 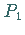 nach
nach 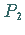 verlaufenden Kurvenabschnitt.
Man beschränkt das Azimut auf das Intervall
verlaufenden Kurvenabschnitt.
Man beschränkt das Azimut auf das Intervall 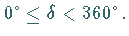
Hinweis: In der Navigation werden die Ortskoordinaten meist in
sexagesimalen Altgraden, sphärische Abstände sowie Kurswinkel und Azimute
dagegen in dezimalen Altgraden angegeben.