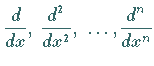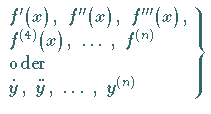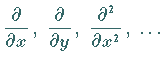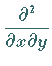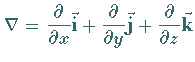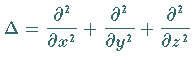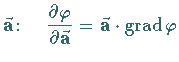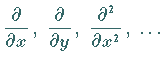Differenz, Ableitungen, Differentialoperatoren

	Differenz oder Zuwachs, z.B.:
	Differential, z.B.:
	Bildung der ersten, zweiten, , -ten Ableitung
	erste, zweite,-te Ableitung der Funktion

	Bildung der ersten, zweiten, , 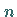-ten partiellen Ableitung
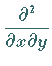	Bildung der zweiten partiellen Ableitung zunächst nach 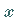, dann nach
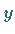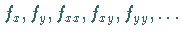	erste, zweite, partielle Ableitung der Funktion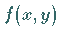
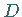	Differentialoperator, z.B.: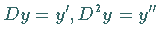
	Gradient eines skalaren Feldes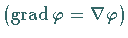
	Divergenz eines Vektorfeldes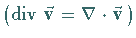
	Rotation eines Vektorfeldes
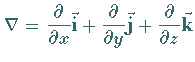	Nablaoperator, hier in kartesischen Koordinaten (auch HAMILTONscher
	Differentialoperator genannt, nicht zu verwechseln mit dem HAMILTON-
	Operator der Quantenmechanik)
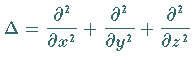	LAPLACE-Operator
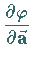	Richtungsableitung, d.h. Ableitung eines skalaren Feldes 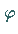nach der
	Richtung des Vektors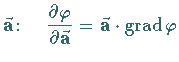