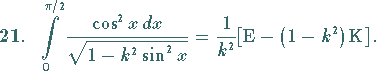Bestimmte Integrale trigonometrischer Funktionen
Für natürliche Zahlen 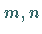 gilt:
gilt:
 |
(21.20) |
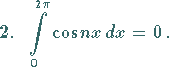 |
(21.21) |
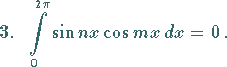 |
(21.22) |
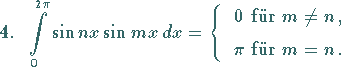 |
(21.23) |
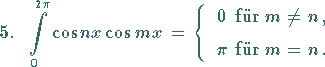 |
(21.24) |
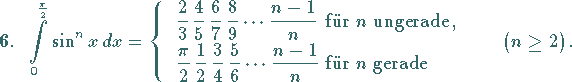 |
(21.25) |
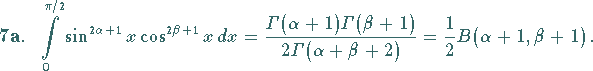 |
(21.26a) |
Mit 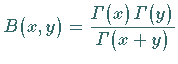 ist die Betafunktion
oder das EULERsche Integral 1. Gattung bezeichnet, mit
ist die Betafunktion
oder das EULERsche Integral 1. Gattung bezeichnet, mit 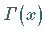 die
Gammafunktion oder das EULERsche Integral 2. Gattung.
die
Gammafunktion oder das EULERsche Integral 2. Gattung.
Diese Formel gilt für beliebige 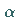 und
und 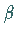 ;
man verwendet sie z.B.
zur Bestimmung der Integrale
;
man verwendet sie z.B.
zur Bestimmung der Integrale
Für 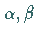 ganzzahlig und positiv ergibt sich:
ganzzahlig und positiv ergibt sich:
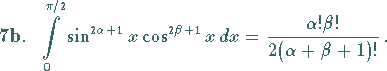 |
(21.26b) |
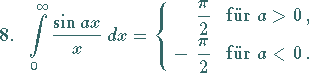 |
(21.27) |
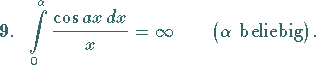 |
(21.28) |
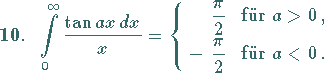 |
(21.29) |
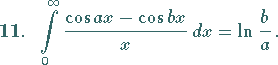 |
(21.30) |
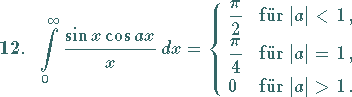 |
(21.31) |
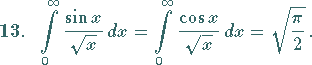 |
(21.32) |
 |
(21.33) |
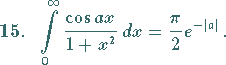 |
(21.34) |
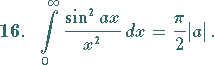 |
(21.35) |
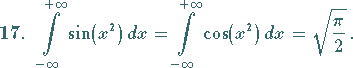 |
(21.36) |
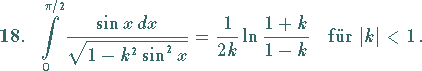 |
(21.37) |
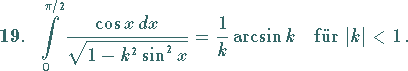 |
(21.38) |
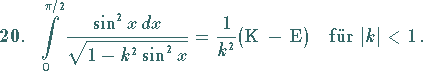 |
(21.39) |
In diesem und dem folgenden Integral sind E und K vollständige elliptische
Integrale:
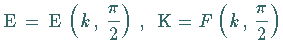 (s. auch Tabelle Elliptische Integrale).
(s. auch Tabelle Elliptische Integrale).
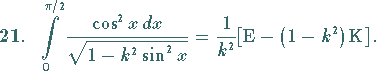 |
(21.40) |
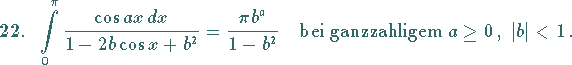 |
(21.41) |
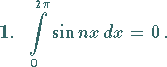
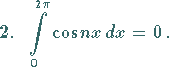
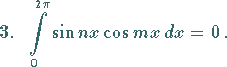
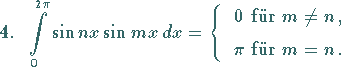
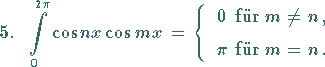
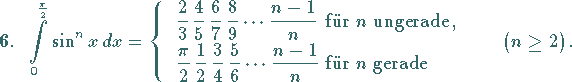
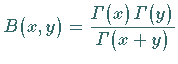 ist die Betafunktion
oder das EULERsche Integral 1. Gattung bezeichnet, mit
ist die Betafunktion
oder das EULERsche Integral 1. Gattung bezeichnet, mit ![]() und
und ![]() ;
man verwendet sie z.B.
zur Bestimmung der Integrale
;
man verwendet sie z.B.
zur Bestimmung der Integrale
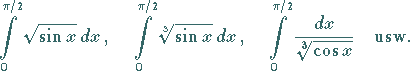
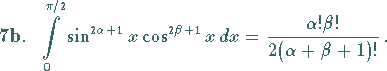
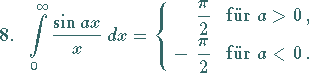
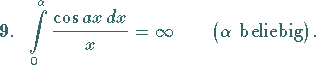
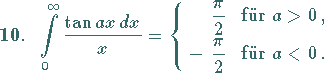
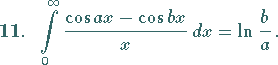
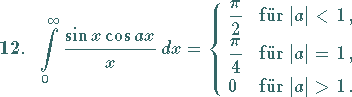
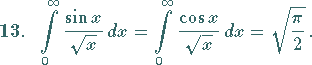

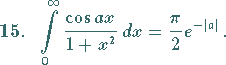
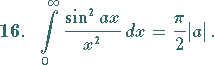
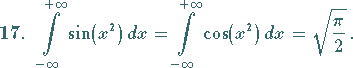
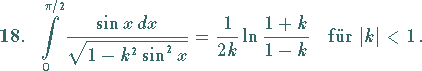
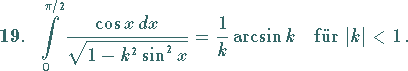
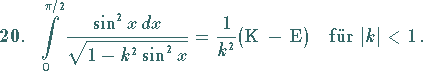
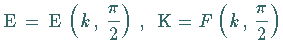 (s. auch Tabelle Elliptische Integrale).
(s. auch Tabelle Elliptische Integrale).