Maple kennt die in der folgenden Tabelle aufgeführten Grundtypen von Zahlen.
Mit Hilfe der Typprüfungsfunktionen gemäß Tabelle können weitere Eigenschaften
ganzer Zahlen erfragt werden:
1. Rationale Zahlen (Typ 
):
Rationale Zahlen sind in Maple die ganzen Zahlen und die Brüche, wobei ein Bruch,
der zur ganzen Zahl vereinfacht werden kann, von Maple nicht als Bruch
(Typ 
)
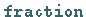erkannt wird.
2. Gleitpunktzahlen (Typ 
):
Setzt man hinter eine ganze Zahl den Dezimalpunkt (
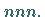), so wird sie automatisch als
Gleitpunktzahl interpretiert.
3. Gemeinsamkeiten:
Alle drei Zahlenarten haben die Typen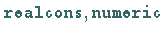 
und
.
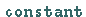Die letzten beiden Typen treffen auch für komplexe Zahlen zu.
4. Komplexe Zahlen:
Komplexe Zahlen werden mit der imaginären Einheit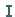 
wie üblich gebildet.
Die Zahl
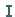ist vom Typ 
,
also die Wurzel einer rationalen
Zahl.
Ihre Definition lautet intern
 |
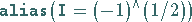(20.34) |
Der hier verwendete Befehl 
bietet die Möglichkeit, abkürzende
Benennungen für Funktionen, Definitionen und andere mathematische Symbole einzuführen.
Er ist in der Form
 |
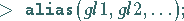(20.35) |
aufzurufen.
Hier sind die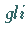 
Gleichungen, die das abkürzende Symbol über vorhandenen
Maple-Funktionen definieren.
Beim Aufruf der Funktion zeigt Maple neben der gerade definierten Abkürzung auch
alle anderen schon vorhandenen
an.
Will man die Abkürzung wieder aufheben, so ist 
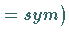aufzurufen.
Kette beliebig vieler Ziffern
Bruch zweier ganzer Zahlen
oder in wissenschaftlicher Notation
