|
|
|
|
| (20.26a) |
| (20.26b) |
Der zweite Befehl evaluiert den Ausdruck, solange ![]() den Wert
den Wert ![]() besitzt.
besitzt.
| Beispiel | |
|
Zur Berechnung eines Näherungswertes von | |
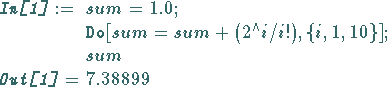 |
(20.27) |
Die ![]() -Schleife evaluiert entsprechend einer vorgegebenen Anzahl, die
-Schleife evaluiert entsprechend einer vorgegebenen Anzahl, die
![]() -Schleife dagegen so lange, bis die vorgebene Bedingung ungültig
wird.
-Schleife dagegen so lange, bis die vorgebene Bedingung ungültig
wird.
Mathematica bietet insbesondere für die Programmierung die Möglichkeit, Variable lokal zu definieren und zu nutzen. Das geschieht mit der Anweisung
| (20.28) |
| Beispiel A | |
|
Es ist eine Prozedur (Funktion) zu definieren, die die Summe der Quadratwurzeln von | |
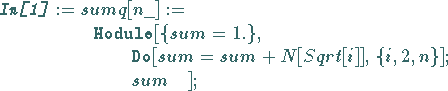 |
(20.29) |
Die eigentliche Stärke der Programmiermöglichkeiten in Mathematica liegt
allerdings in der Nutzung funktionaler Methoden der Programmierung, die mit den
Operationen ![]() und weiteren möglich werden.
und weiteren möglich werden.
| Beispiel B | |
|
Beispiel A läßt sich funktional für den Fall, daß eine Genauigkeit auf
10 Ziffern gefordert ist, folgendermaßen schreiben:
| |
Für Einzelheiten muß auf Lit. 20.6 verwiesen werden.
|
|
|