Analytische Bedingung für die Unabhängigkeit
Im Falle zweier Funktionen 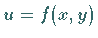 und
und 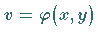 darf ihre
Funktionaldeterminante
darf ihre
Funktionaldeterminante
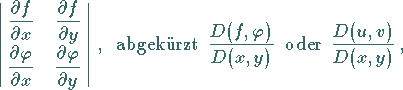 |
(2.272a) |
in dem betrachteten Gebiet nicht identisch verschwinden.
Analog gilt im Fall von 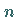 Funktionen mit
Funktionen mit 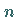 Veränderlichen
Veränderlichen
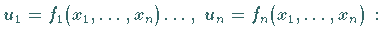
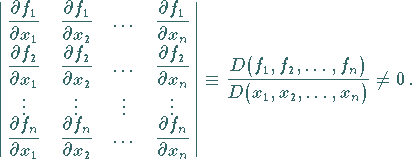 |
(2.272b) |
Wenn die Anzahl 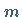 der Funktionen
der Funktionen 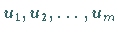 kleiner ist als die
Anzahl
kleiner ist als die
Anzahl 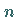 der Veränderlichen
der Veränderlichen 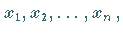 dann sind diese
Funktionen unabhängig, sofern wenigstens eine Unterdeterminante
dann sind diese
Funktionen unabhängig, sofern wenigstens eine Unterdeterminante 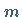 -ter
Ordnung der folgenden Matrix nicht verschwindet.
-ter
Ordnung der folgenden Matrix nicht verschwindet.
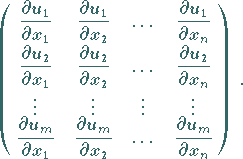 |
(2.272c) |
Die Anzahl der unabhängigen Funktionen ist gleich dem
Rang 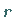 dieser Matrix.
Hierbei werden diejenigen Funktionen unabhängig sein, deren Ableitung als Elemente in
der nicht identisch verschwindenden Unterdeterminante
dieser Matrix.
Hierbei werden diejenigen Funktionen unabhängig sein, deren Ableitung als Elemente in
der nicht identisch verschwindenden Unterdeterminante 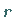 -ter Ordnung stehen.
-ter Ordnung stehen.
Wenn 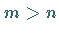 ist, dann können von den gegebenen
ist, dann können von den gegebenen 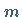 Funktionen höchstens
Funktionen höchstens 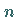 unabhängig sein.
unabhängig sein.
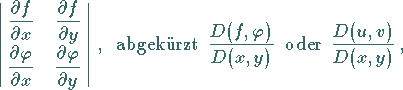
![]() Funktionen mit
Funktionen mit ![]() Veränderlichen
Veränderlichen
![]()
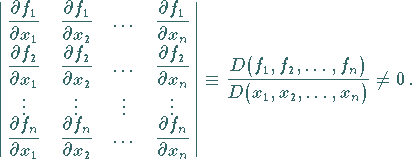
![]() der Funktionen
der Funktionen ![]() kleiner ist als die
Anzahl
kleiner ist als die
Anzahl ![]() der Veränderlichen
der Veränderlichen ![]() dann sind diese
Funktionen unabhängig, sofern wenigstens eine Unterdeterminante
dann sind diese
Funktionen unabhängig, sofern wenigstens eine Unterdeterminante ![]() -ter
Ordnung der folgenden Matrix nicht verschwindet.
-ter
Ordnung der folgenden Matrix nicht verschwindet.
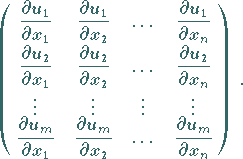
![]() dieser Matrix.
Hierbei werden diejenigen Funktionen unabhängig sein, deren Ableitung als Elemente in
der nicht identisch verschwindenden Unterdeterminante
dieser Matrix.
Hierbei werden diejenigen Funktionen unabhängig sein, deren Ableitung als Elemente in
der nicht identisch verschwindenden Unterdeterminante ![]() -ter Ordnung stehen.
-ter Ordnung stehen.
![]() ist, dann können von den gegebenen
ist, dann können von den gegebenen ![]() Funktionen höchstens
Funktionen höchstens ![]() unabhängig sein.
unabhängig sein.