Definition des Grenzwertes einer Funktion
Die Funktion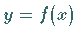 
sei in einer Umgebung von 
,
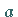eventuell mit Ausnahme
von ,
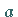definiert.
Die Funktion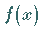 
besitzt an der Stelle 
den Grenzwert oder
Limes 
,
in Zeichen
 |
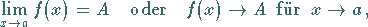(2.14) |
wenn sich die Funktion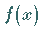
bei unbegrenzter Annäherung von 
an 
unbegrenzt
an
nähert.
Die Funktion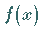
braucht an der Stelle
den Wert
nicht anzunehmen und
braucht an dieser Stelle auch nicht definiert zu sein.
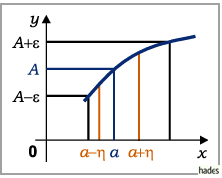
Exakte Formulierung: Der Grenzwert (2.14) existiert,
wenn sich nach Vorgabe einer beliebig kleinen positiven Zahl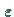 
eine
zweite positive Zahl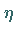 
derart finden läßt, daß für alle
mit
 |
(2.15) |
eventuell mit Ausnahme des Punktes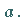 
Wenn
Randpunkt eines zusammenhängenden Gebietes ist, reduziert sich die Ungleichung
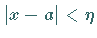zu einer der beiden einfachen Ungleichungen 
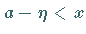oder
.
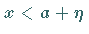