Die Vorgehensweise wird am Beispiel der Arkussinusfunktion gezeigt, die in der ersten der
vier folgenden Abbildungen dargestellt ist.
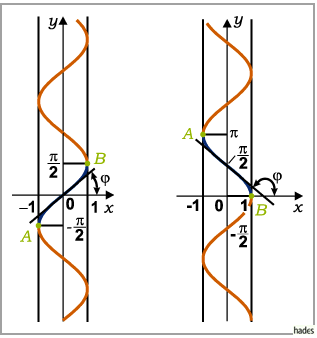
Der Definitionsbereich von 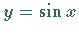 wird in die Monotonieintervalle
wird in die Monotonieintervalle
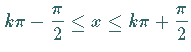 mit
mit
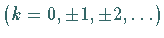 zerlegt.
Spiegelung von
zerlegt.
Spiegelung von 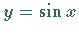 an der Winkelhalbierenden
an der Winkelhalbierenden 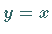 liefert die Umkehrfunktionen
liefert die Umkehrfunktionen
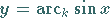 |
(2.132a) |
mit den Definitions- und Wertebereichen
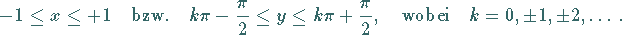 |
(2.132b) |
Die Schreibweise 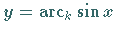 ist gleichbedeutend mit
ist gleichbedeutend mit 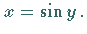 Analog erhält man die übrigen Arkusfunktionen
Analog erhält man die übrigen Arkusfunktionen 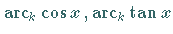 und
und
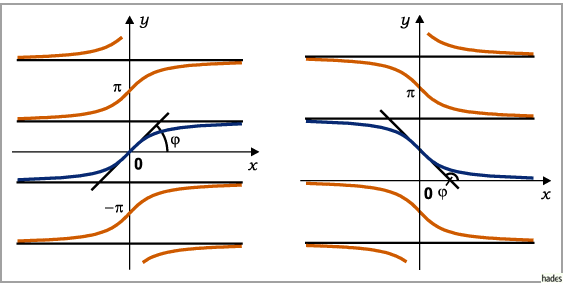
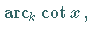 die in der zweiten, dritten und vierten Abbildungen dargestellt sind.
Die Definitions- und Wertebereiche der Arkusfunktionen und die gleichbedeutenden
trigonometrischen Funktionen sind in der folgenden Tabelle aufgeführt.
die in der zweiten, dritten und vierten Abbildungen dargestellt sind.
Die Definitions- und Wertebereiche der Arkusfunktionen und die gleichbedeutenden
trigonometrischen Funktionen sind in der folgenden Tabelle aufgeführt.
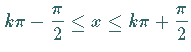 mit
mit
![]() ist gleichbedeutend mit
ist gleichbedeutend mit ![]() Analog erhält man die übrigen Arkusfunktionen
Analog erhält man die übrigen Arkusfunktionen ![]() und
und
![]() die in der zweiten, dritten und vierten Abbildungen dargestellt sind.
Die Definitions- und Wertebereiche der Arkusfunktionen und die gleichbedeutenden
trigonometrischen Funktionen sind in der folgenden Tabelle aufgeführt.
die in der zweiten, dritten und vierten Abbildungen dargestellt sind.
Die Definitions- und Wertebereiche der Arkusfunktionen und die gleichbedeutenden
trigonometrischen Funktionen sind in der folgenden Tabelle aufgeführt.