Gewöhnliches Iterationsverfahren
Zur Lösung einer Gleichung, die auf die Fixpunktform 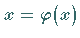 gebracht
worden ist, verwendet man die naheliegende Iterationsvorschrift
gebracht
worden ist, verwendet man die naheliegende Iterationsvorschrift
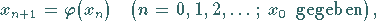 |
(19.3) |
die als gewöhnliches Iterationsverfahren bezeichnet wird.
Es konvergiert gegen eine Lösung 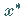 ,
wenn es eine Umgebung von
,
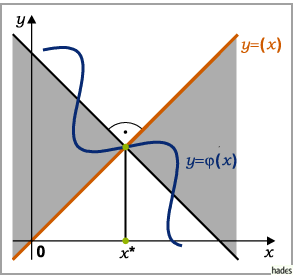
wenn es eine Umgebung von 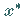 (s. Abbildung) mit
(s. Abbildung) mit
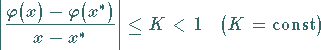 |
(19.4) |
gibt und die Ausgangsnäherung 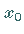 in dieser Umgebung liegt.
in dieser Umgebung liegt.
Ist 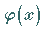 differenzierbar, dann lautet die entsprechende Bedingung
differenzierbar, dann lautet die entsprechende Bedingung
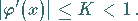 |
(19.5) |
Die Konvergenz des gewöhnlichen Iterationsverfahrens ist um so besser, je kleiner die
Zahl 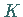 ist.
ist.
| Beispiel |
|
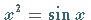 ,
d.h. ,
d.h. 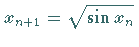 . .
|
Hinweise:
1. Im Falle komplexer Lösungen setzt man 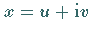 .
Durch Trennung von Real- und Imaginärteil geht die zu lösende Gleichung in ein System
zweier Gleichungen für die reellen Unbekannten
.
Durch Trennung von Real- und Imaginärteil geht die zu lösende Gleichung in ein System
zweier Gleichungen für die reellen Unbekannten 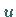 und
und 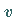 über.
über.
2. Die iterative Lösung nichtlinearer Gleichungssysteme wird in Abschnitt
Nichtlineare Gleichungen behandelt.
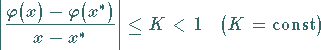
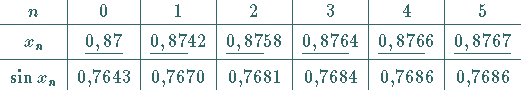
![]() .
Durch Trennung von Real- und Imaginärteil geht die zu lösende Gleichung in ein System
zweier Gleichungen für die reellen Unbekannten
.
Durch Trennung von Real- und Imaginärteil geht die zu lösende Gleichung in ein System
zweier Gleichungen für die reellen Unbekannten ![]() und
und ![]() über.
über.