Dynamische Optimierungsprobleme
Das Ziel besteht nun in der Ermittlung einer Politik
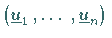 ,
die unter Beachtung aller
Nebenbedingungen den Zustand
,
die unter Beachtung aller
Nebenbedingungen den Zustand 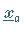 in den Zustand
in den Zustand 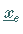 überführt und dabei eine Zielfunktion bzw. Kostenfunktion
überführt und dabei eine Zielfunktion bzw. Kostenfunktion
 minimiert.
Die Funktionen
minimiert.
Die Funktionen 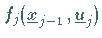 werden als
Stufenkosten bezeichnet.
Damit lautet das dynamische Optimierungsproblem in der Standardform
werden als
Stufenkosten bezeichnet.
Damit lautet das dynamische Optimierungsproblem in der Standardform
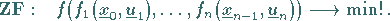 |
(18.115a) |
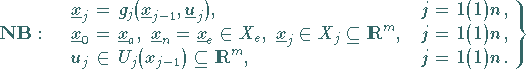 |
(18.115b) |
Die Beziehungen (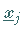 )
heißen dynamische und die Beziehungen
(
)
heißen dynamische und die Beziehungen
(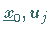 )
statische Nebenbedingungen .
Alternativ zu (18.115a) kann auch ein Maximumproblem vorliegen.
Eine Politik
)
statische Nebenbedingungen .
Alternativ zu (18.115a) kann auch ein Maximumproblem vorliegen.
Eine Politik 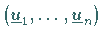 ,
die alle Nebenbedingungen
erfüllt, wird als zulässig bezeichnet.
Um die Methoden der dynamischen Optimierung anwenden zu können, werden im Abschnitt
Bellmannsche Funktionalgleichungen einige Forderungen an die
Form der Kostenfunktion gestellt.
,
die alle Nebenbedingungen
erfüllt, wird als zulässig bezeichnet.
Um die Methoden der dynamischen Optimierung anwenden zu können, werden im Abschnitt
Bellmannsche Funktionalgleichungen einige Forderungen an die
Form der Kostenfunktion gestellt.
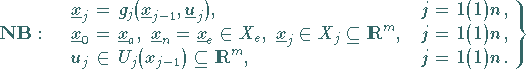
![]() )
heißen dynamische und die Beziehungen
(
)
heißen dynamische und die Beziehungen
(![]() )
statische Nebenbedingungen .
Alternativ zu (18.115a) kann auch ein Maximumproblem vorliegen.
Eine Politik
)
statische Nebenbedingungen .
Alternativ zu (18.115a) kann auch ein Maximumproblem vorliegen.
Eine Politik ![]() ,
die alle Nebenbedingungen
erfüllt, wird als zulässig bezeichnet.
Um die Methoden der dynamischen Optimierung anwenden zu können, werden im Abschnitt
Bellmannsche Funktionalgleichungen einige Forderungen an die
Form der Kostenfunktion gestellt.
,
die alle Nebenbedingungen
erfüllt, wird als zulässig bezeichnet.
Um die Methoden der dynamischen Optimierung anwenden zu können, werden im Abschnitt
Bellmannsche Funktionalgleichungen einige Forderungen an die
Form der Kostenfunktion gestellt.