Ein Punkt 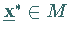 genügt den lokalen KUHN- TUCKER-Bedingungen,
wenn Zahlen
genügt den lokalen KUHN- TUCKER-Bedingungen,
wenn Zahlen 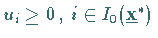 ,
existieren, für die gilt
,
existieren, für die gilt
die Indexmenge der in 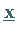 aktiven Restriktionen ist.
aktiven Restriktionen ist.
Der Punkt 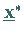 heißt dann auch KUHN- TUCKER-Punkt
oder stationärer Punkt .
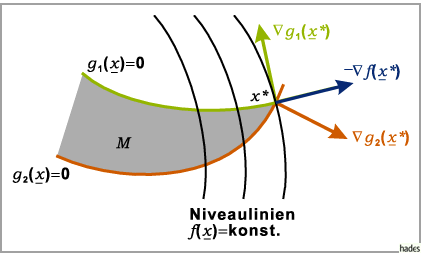
Geometrisch betrachtet erfüllt ein Punkt
heißt dann auch KUHN- TUCKER-Punkt
oder stationärer Punkt .
Geometrisch betrachtet erfüllt ein Punkt 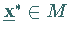 die lokalen
KUHN- TUCKER-Bedingungen, wenn der negative Gradient
die lokalen
KUHN- TUCKER-Bedingungen, wenn der negative Gradient
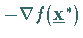 in dem durch die Gradienten der in
in dem durch die Gradienten der in 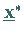 aktiven
Nebenbedingungen
aktiven
Nebenbedingungen 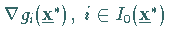 ,
aufgespannten
Kegel liegt (s. Abbildung).
,
aufgespannten
Kegel liegt (s. Abbildung).
Oft wird die folgende äquivalente Formulierung für (18.39a,b) verwendet:
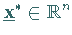 genügt den lokalen KUHN- TUCKER-Bedingungen, wenn
ein
genügt den lokalen KUHN- TUCKER-Bedingungen, wenn
ein 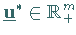 existiert, so daß gilt
existiert, so daß gilt
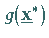 |
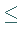 |
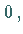 |
(18.40a) |
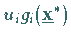 |
 |
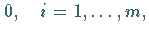 |
(18.40b) |
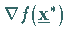 |
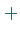 |
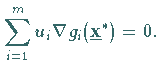 |
(18.40c) |
![]() heißt dann auch KUHN- TUCKER-Punkt
oder stationärer Punkt .
Geometrisch betrachtet erfüllt ein Punkt
heißt dann auch KUHN- TUCKER-Punkt
oder stationärer Punkt .
Geometrisch betrachtet erfüllt ein Punkt ![]() die lokalen
KUHN- TUCKER-Bedingungen, wenn der negative Gradient
die lokalen
KUHN- TUCKER-Bedingungen, wenn der negative Gradient
![]() in dem durch die Gradienten der in
in dem durch die Gradienten der in ![]() aktiven
Nebenbedingungen
aktiven
Nebenbedingungen ![]() ,
aufgespannten
Kegel liegt (s. Abbildung).
,
aufgespannten
Kegel liegt (s. Abbildung).