1. Kegel der zulässigen Richtungen Der Kegel der zulässigen Richtungen in
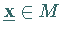 ist definiert durch
ist definiert durch
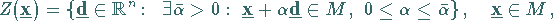 |
(18.34) |
wobei Richtungen mit 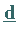 bezeichnet sind.
Ist
bezeichnet sind.
Ist 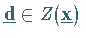 ,
dann liegen alle Punkte des Strahls
,
dann liegen alle Punkte des Strahls
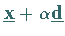 für hinreichend kleine
für hinreichend kleine 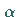 -Werte in
-Werte in 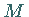 .
.
2. Abstiegsrichtung Eine Abstiegsrichtung im Punkt 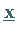 ist ein Vektor
ist ein Vektor
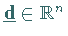 ,
für den es ein
,
für den es ein 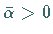 gibt mit:
gibt mit:
 |
(18.35) |
In einem Minimalpunkt existiert keine Abstiegsrichtung, die zugleich auch zulässig ist.
Ist 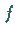 differenzierbar, so folgt aus
differenzierbar, so folgt aus 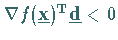 die
Abstiegseigenschaft der Richtung
die
Abstiegseigenschaft der Richtung 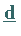 .
Mit
.
Mit  ist der Nablaoperator bezeichnet, so daß
ist der Nablaoperator bezeichnet, so daß 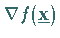 den
Gradienten der skalaren Funktion
den
Gradienten der skalaren Funktion 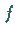 an der Stelle
an der Stelle 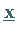 darstellt.
darstellt.
![]() differenzierbar, so folgt aus
differenzierbar, so folgt aus ![]() die
Abstiegseigenschaft der Richtung
die
Abstiegseigenschaft der Richtung ![]() .
Mit
.
Mit ![]() ist der Nablaoperator bezeichnet, so daß
ist der Nablaoperator bezeichnet, so daß ![]() den
Gradienten der skalaren Funktion
den
Gradienten der skalaren Funktion ![]() an der Stelle
an der Stelle ![]() darstellt.
darstellt.