a) Besitzen beide Probleme zulässige Punkte, d.h.,
,
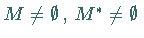dann gilt
 |
(18.21a) |
und für beide Probleme existieren Optimalpunkte.
b) Die Punkte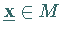 
und 
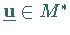sind genau dann
Optimalpunkte des jeweiligen Problems, wenn gilt:
 |
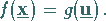(18.21b) |
c) Ist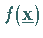 
über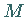 
nach oben bzw. 
über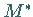 
nach unten unbeschränkt, so ist 
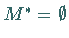bzw.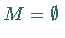 
.
d) Die Punkte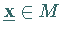
und
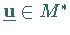sind genau dann
Optimalpunkte der jeweiligen Aufgaben, wenn gilt:
 |
(18.21c) |
An Hand der letzten beiden Beziehungen kann man aus einer nicht entarteten
Optimallösung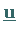 
des dualen Problems eine Lösung 
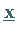des primalen
Problems aus dem folgenden linearen Gleichungssystem ermitteln:
 |
 |
 |
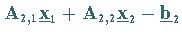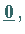(18.22a) |
 |
|
 |
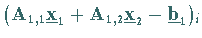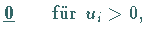(18.22b) |
 |
|
 |
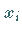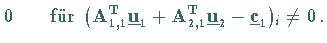(18.22c) |
Zur Lösung des dualen Problems kann das Simplexverfahren verwendet werden.
