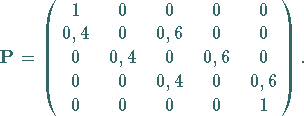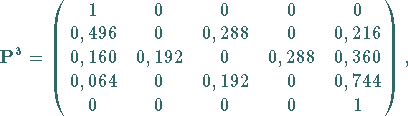|
Ein Teilchen verändere seine Lage (Zustand) 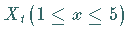 längs
einer Geraden zu den Zeitpunkten
längs
einer Geraden zu den Zeitpunkten 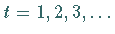 nach der folgenden Vorschrift:
nach der folgenden Vorschrift:
1. Von den Punkten 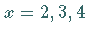 wird es in der nachfolgenden Zeiteinheit um eine
Einheit mit der Wahrscheinlichkeit
wird es in der nachfolgenden Zeiteinheit um eine
Einheit mit der Wahrscheinlichkeit 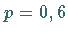 nach rechts und mit der Wahrscheinlichkeit
nach rechts und mit der Wahrscheinlichkeit
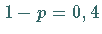 nach links verschoben.
nach links verschoben.
2. An den Punkte 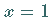 und
und 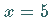 wird das Teilchen absorbiert, d.h., es bleibt mit
der Wahrscheinlichkeit
wird das Teilchen absorbiert, d.h., es bleibt mit
der Wahrscheinlichkeit 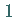 in der nachfolgenden Zeit dort.
in der nachfolgenden Zeit dort.
3. Zur Zeit  befinde sich das Teilchen an der Stelle
befinde sich das Teilchen an der Stelle  .
Die Wahrscheinlichkeitsverteilung .
Die Wahrscheinlichkeitsverteilung 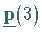 zum Zeitpunkt
zum Zeitpunkt  ist zu
berechnen.
ist zu
berechnen.
Gemäß (16.118) gilt 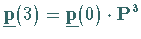 mit
mit 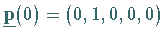 und der Übergangsmatrix
und der Übergangsmatrix
Daraus folgt
und man erhält 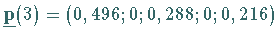 . .
|