Hängt bei einer stochastischen Kette die Wahrscheinlichkeit eines Ereignisses
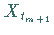nur vom Zustand zum Zeitpunkt 
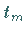ab, so spricht man von einer
MARKOFFschen Kette , d.h., es gilt
Es seien eine MARKOFFsche Kette sowie die zwei Zeitpunkte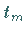
und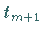 
gegeben.
Die bedingten Wahrscheinlichkeiten
 |
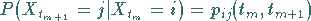(16.110) |
heißen Übergangswahrscheinlichkeiten .
Die Übergangswahrscheinlichkeit gibt an, mit welcher Wahrscheinlichkeit der Zustand
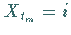bei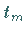
in den Zustand 
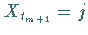bei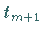
übergeht.
Ist der Zustandsraum einer MARKOFFschen Kette endlich, d.h.
,
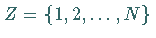so lassen sich die Übergangswahrscheinlichkeiten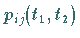 
zwischen den Zuständen zum Zeitpunkt 
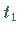und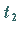 
in einer quadratischen Matrix
,
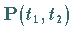der sogenannten Übergangsmatrix ,
darstellen:
 |
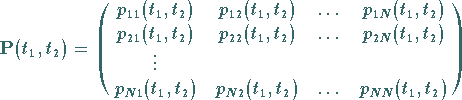(16.111) |
Die Zeitpunkte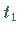
und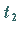
müssen nicht aufeinanderfolgende Zeitpunkte sein.
