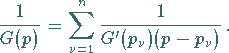|
|
|
|
auf,
wobei 
ein Polynom in 
darstellt.
Hat man die Originalfunktionen zu 
und 
gefunden, dann erhält man
die gesuchten Originalfunktionen zu 
durch Anwendung des Faltungssatzes.
:
Hat die Bildfunktion
nur einfache Pole 
,
dann gilt für sie die Partialbruchzerlegung
 |
(15.39) |
Daher lautet die zugehörige Originalfunktion
 |
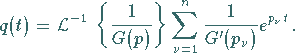(15.40) |
3. Heavysidescher Entwicklungssatz:
Ist die Zählerfunktion
ebenfalls ein Polynom von 
,
aber von niedrigerem
Grade als 
,
dann erhält man die Originalfunktion zu
mit Hilfe der nach
HEAVYSIDE benannten Formel
 |
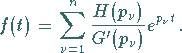(15.41) |
4. Komplexe Nullstellen:
Treten komplexe Wurzeln im Nenner auf, dann kann man den HEAVYSIDEschen
Entwicklungssatz in der gleichen Weise anwenden.
Man kann auch jeweils konjugiert komplexe Glieder, die im Falle komplexer Nullstellen
stets vorhanden sein müssen, zu einem quadratischen Ausdruck zusammenfassen, dessen
Rücktransformation wie auch im Falle mehrfacher Nullstellen von
mit Hilfe der
Tabelle der Korrespondenzen durchgeführt werden kann.
| Beispiel | |
|
| |
|
|
,
d.h. 
,
.
sind sämtlich einfach.
Nach dem HEAVISIDEschen Satz erhält man
.
sind identisch.