WALSH-Systeme
Analog zu den trigonometrischen Funktionen werden periodische
Treppenfunktionen betrachtet.
Man verwendet das Intervall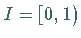 
als Periodenintervall und unterteilt
es in 
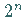gleichlange Teilintervalle.
Sei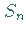 
die Menge der periodischen Treppenfunktionen mit der Periode 1
über einer solchen Intervallteilung.
Die zu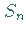
gehörenden Treppenfunktionen kann man als Vektoren eines
endlichdimensionalen Vektorraumes auffassen, denn jede Funktion 
wird durch ihre Werte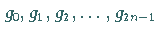 
in den
Teilintervallen bestimmt und kann demzufolge als Vektor aufgefaßt
werden:
 |
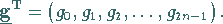(15.157) |
Die zu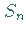
gehörenden WALSH-Funktionen bilden mit einem geeigneten
Skalarprodukt eine orthogonale Basis in diesem Raum.
Die Basisvektoren können auf verschiedene Weise numeriert werden, so
daß man sehr viele WALSH-Systeme erhält, die aber alle dieselben
Funktionen enthalten.
Es zeigt sich aber, daß drei Systeme zu bevorzugen sind:
WALSH- KRONECKER-Funktionen, WALSH- KACZMARZ-Funktionen und
WALSH- PALEY-Funktionen.
In Analogie zur FOURIER-Transformation wird die
WALSH- Transformation aufgebaut, wobei die Rolle der trigonometrischen
Funktionen von den WALSH-Funktionen übernommen wird.
Man erhält z.B. WALSH-Reihen, WALSH-Polynome, WALSH-Sinus- und
WALSH-Kosinus-Transformationen, WALSH-Integrale, und analog zur
schnellen FOURIER-Transfornmation gibt es die schnelle WALSH-Transformation.
Eine Einführung in Theorie und Anwendung der WALSH-Funktionen s. Lit. 15.7.
