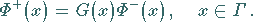 |
(11.84) |
Die Funktion 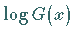 ändert ihren Wert bei einmaligem Durchlauf der Kurve
ändert ihren Wert bei einmaligem Durchlauf der Kurve
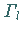 um den Wert
um den Wert 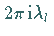 ,
wobei
,
wobei 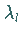 eine
ganze Zahl ist.
Die Wertänderung von
eine
ganze Zahl ist.
Die Wertänderung von 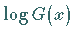 bei einmaligem Durchlauf des gesamten Kurvensystems
bei einmaligem Durchlauf des gesamten Kurvensystems
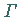 beträgt dann
beträgt dann
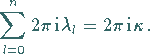 |
(11.85a) |
Die Zahl  wird als
Index des HILBERTschen Problems bezeichnet.
Es wird die Funktion
wird als
Index des HILBERTschen Problems bezeichnet.
Es wird die Funktion
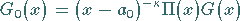 |
(11.85b) |
mit
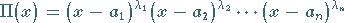 |
(11.85c) |
gebildet, wobei 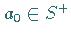 und
und 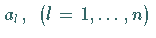 ,
aus dem Inneren
von
,
aus dem Inneren
von 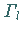 beliebig, aber fest gewählt sind.
Ist
beliebig, aber fest gewählt sind.
Ist 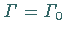 eine einfache geschlossene Kurve (
eine einfache geschlossene Kurve ( ), dann wird
), dann wird
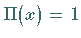 gesetzt.
Mit
gesetzt.
Mit
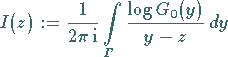 |
(11.85d) |
erhält man folgende spezielle Lösung des homogenen HILBERTschen Problems, auch
Grundlösung genannt:
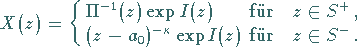 |
(11.85e) |
Die allgemeinste Lösung des homogenen HILBERTschen Problems, die nicht im
Unendlichen verschwindet, lautet für 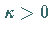
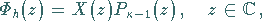 |
(11.86) |
mit einem beliebigen Polynom 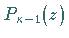 höchstens (
höchstens (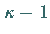 )-ten Grades.
Für
)-ten Grades.
Für 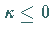 existiert nur die triviale Lösung
existiert nur die triviale Lösung 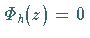 .
Im Falle
.
Im Falle 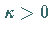 besitzt das homogene HILBERTsche Problem
besitzt das homogene HILBERTsche Problem 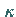 linear
unabhängige, im Unendlichen verschwindende Lösungen.
linear
unabhängige, im Unendlichen verschwindende Lösungen.
![]()