Definition
Unter dem Logarithmus einer Zahl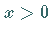 
zur
Basis 
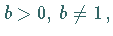oder als Formel geschrieben
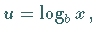wird der Exponent der Potenz verstanden,
in die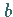 
zu erheben ist, um die Zahl 
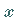zu erhalten.
Folglich ergibt sich aus der Gleichung
 |
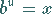(1.21a) |
die Gleichung
 |
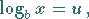(1.21b) |
und umgekehrt folgt aus der zweiten die erste Gleichung.
Speziell gilt
 |
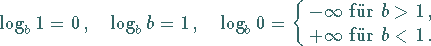(1.21c) |
Zur Ausdehnung des Logarithmus auf negative Argumentwerte bedarf es der komplexen
Zahlen.
Logarithmieren einer gegebenen Größe bedeutet das Aufsuchen ihres
Logarithmus.
Man versteht darunter auch die Umwandlung logarithmischer Ausdrücke gemäß
(1.22a, 1.22b).
Das Aufsuchen einer Größe aus ihrem Logarithmus wird Potenzieren
genannt.
