Gleichungen 4. Grades
1. Normalform:
 |
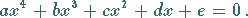(1.161) |
Sind alle Koeffizienten dieser Gleichung reell, dann hat sie keine oder 2 oder 4 reelle
Lösungen.
2. Spezielle Formen:
Wenn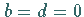 
ist, dann können die Wurzeln von
 |
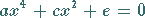(1.162a) |
mit Hilfe der Formeln
 |
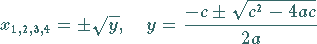(1.162b) |
berechnet werden.
Für 
und 
werden die Wurzeln der Gleichung
 |
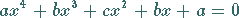(1.162c) |
mit Hilfe der Formeln
 |
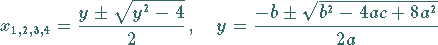(1.162d) |
berechnet.
Hinweis: Zur Lösung der allgemeinen Gleichung 4. Grades werden in den nächsten
beiden Abschnitten zwei Methoden betrachtet.
Eine dritte Lösungsmethode beruht auf Näherungsverfahren.
